por gasparina nunes » Sáb Abr 07, 2012 23:42
por fraol » Dom Abr 08, 2012 00:42
, então 
.
, então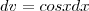 
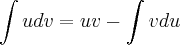, agora basta substituir os dados acima e rearranjar.
.
.
por gasparina nunes » Dom Abr 08, 2012 22:22
por fraol » Dom Abr 08, 2012 22:43
gasparina nunes escreveu:Calcule a área compreendida entre a função y=?x e o eixo do x, no intervalo 0 ? x ? 4
![A = \int_{0}^{4} \sqrt{x} dx = \left[ \frac{2x^{\frac{3}{2}}}{3} \right]_0^4 = \frac{2.4^{\frac{3}{2}}}{3}](/latexrender/pictures/44ab32c3353bc80f292b5e0124695d0c.png "A = \int_{0}^{4} \sqrt{x} dx = \left[ \frac{2x^{\frac{3}{2}}}{3} \right]_0^4 = \frac{2.4^{\frac{3}{2}}}{3}")
Voltar para Cálculo: Limites, Derivadas e Integrais
por liviatoniolo222 » Seg Mai 21, 2018 22:54
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)