 por Toketsu » Ter Mar 27, 2012 16:26
por Toketsu » Ter Mar 27, 2012 16:26
Dados log 5 = 0,70 e log 3 = 0,48, calcule o valor de x na equação
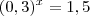
. Eu transformei 0,3 em

e o mesmo com 1,5. Apliquei os logaritmos e encontrei aproximadamente 2,46. Mas o resultado no livro mostra como -0,35. Alguém poderia resolver e me mostrar o meu erro? Obrigado.
-
Toketsu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 27, 2012 16:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por fraol » Ter Mar 27, 2012 18:42
por fraol » Ter Mar 27, 2012 18:42
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- Exercício de logaritmo
por Aliocha Karamazov » Sáb Abr 09, 2011 01:24
- 2 Respostas
- 1358 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Abr 09, 2011 01:54
Logaritmos
-
- Exercício de logaritmo
por Aliocha Karamazov » Seg Abr 11, 2011 22:15
- 7 Respostas
- 4096 Exibições
- Última mensagem por Aliocha Karamazov

Ter Abr 12, 2011 18:17
Logaritmos
-
- Exercicio de Logaritmo...
por torilleon » Qui Fev 16, 2012 18:47
- 1 Respostas
- 1170 Exibições
- Última mensagem por ant_dii

Qui Fev 16, 2012 18:51
Logaritmos
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1846 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
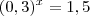 . Eu transformei 0,3 em
. Eu transformei 0,3 em  e o mesmo com 1,5. Apliquei os logaritmos e encontrei aproximadamente 2,46. Mas o resultado no livro mostra como -0,35. Alguém poderia resolver e me mostrar o meu erro? Obrigado.
e o mesmo com 1,5. Apliquei os logaritmos e encontrei aproximadamente 2,46. Mas o resultado no livro mostra como -0,35. Alguém poderia resolver e me mostrar o meu erro? Obrigado.
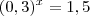 . Eu transformei 0,3 em
. Eu transformei 0,3 em  e o mesmo com 1,5. Apliquei os logaritmos e encontrei aproximadamente 2,46. Mas o resultado no livro mostra como -0,35. Alguém poderia resolver e me mostrar o meu erro? Obrigado.
e o mesmo com 1,5. Apliquei os logaritmos e encontrei aproximadamente 2,46. Mas o resultado no livro mostra como -0,35. Alguém poderia resolver e me mostrar o meu erro? Obrigado.
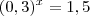 , então:
, então: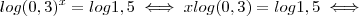
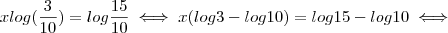
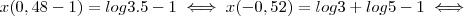
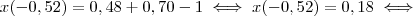
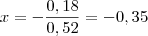 .
.