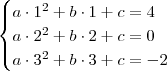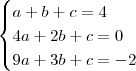por jamesramos » Sáb Mar 10, 2012 17:55
por jamesramos » Sáb Mar 10, 2012 17:55
Boa Tarde, preciso de ajudar nesta Função.

Tem que se determinar o Produto ABC. Eu cheguei em sistemas, mas não consegui resolver por sistemas. Como posso estar resolvendo isso?
Obrigado!
-
jamesramos
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Mar 04, 2012 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Produção
- Andamento: cursando
 por emsbp » Sáb Mar 10, 2012 18:44
por emsbp » Sáb Mar 10, 2012 18:44
Boa noite, José.
Podes ser mais claro no enunciado do problema?
Apenas estás a dar as imagens dos objetos 1, 2 e 3.
Por aí já sabemos que a função muda de sinal, ou seja, é positiva ou nula no intervalo
![\left[1, \right2] \left[1, \right2]](/latexrender/pictures/d4a647053823ba0ae6ce71898f4648b0.png)
e negativa ou nula no intervalo
![\left[2 ,\right3] \left[2 ,\right3]](/latexrender/pictures/d85eb8f44ddacdfeecb8210f22cad768.png)
.
Referes-te ao produto ABC. Mas quem é ABC? São os 3 objetos?
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por jamesramos » Sáb Mar 10, 2012 21:47
por jamesramos » Sáb Mar 10, 2012 21:47
Temos que substituir os valores na Função do 2. Grau (
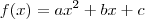
e determinar o produto ABC.
Sabendo que f(1)=4, f(2)=0 e f(3)=-2
-
jamesramos
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Mar 04, 2012 22:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Produção
- Andamento: cursando
 por Alex Paulista » Sáb Mar 10, 2012 22:48
por Alex Paulista » Sáb Mar 10, 2012 22:48
Boa noite Professor,
A minha dúvida, nem sei com perguntar na verdade. Na época da faculdade aprendi a montar ama função quadrática mas não me lembro mais como faz. Sei que o professor dava X e Y (vários pares) nos jogavamos no gráfico e aprtir daí conseguiamos montar a função ax²+bx+c=0. Minha dúvida e como fazer isso, realmente já procurei de todas as formas mas não me recordo de nada mais além disso. Se por acaso puderem me ajudar vou agradecer muito.
Alexandre Paulista
-
Alex Paulista
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Mar 10, 2012 22:41
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel e Ciências Econnômicas
- Andamento: formado
 por LuizAquino » Ter Mar 13, 2012 20:34
por LuizAquino » Ter Mar 13, 2012 20:34
jamesramos escreveu:Boa Tarde, preciso de ajudar nesta Função. f(1)=4, f(2)=0, f(3)= -2
Tem que se determinar o Produto ABC. Eu cheguei em sistemas, mas não consegui resolver por sistemas. Como posso estar resolvendo isso?
(...)
Temos que substituir os valores na Função do 2. Grau (
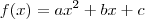
) e determinar o produto ABC.
Sabendo que f(1)=4, f(2)=0 e f(3)=-2
Alex Paulista escreveu:A minha dúvida, nem sei com perguntar na verdade. Na época da faculdade aprendi a montar ama função quadrática mas não me lembro mais como faz. Sei que o professor dava X e Y (vários pares) nos jogavamos no gráfico e aprtir daí conseguiamos montar a função ax²+bx+c=0. Minha dúvida e como fazer isso, realmente já procurei de todas as formas mas não me recordo de nada mais além disso. Se por acaso puderem me ajudar vou agradecer muito.
Vocês devem montar um sistema de equações da seguinte maneira.

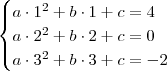
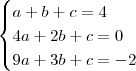
Para resolver esse sistema, eu recomendo que vocês estudem as técnicas abordadas na videoaula "Matemática - Aula 23 - Sistemas Lineares". Essa videoaula está disponível no canal do Nerckie:
http://www.youtube.com/nerckie
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] isso é função do segundo grau?
por maulakalanata » Qua Mar 27, 2013 04:03
- 1 Respostas
- 2280 Exibições
- Última mensagem por timoteo

Qua Mar 27, 2013 10:51
Funções
-
- [Função 1°grau] determinar função.
por Thiago 86 » Ter Abr 23, 2013 11:27
- 2 Respostas
- 2406 Exibições
- Última mensagem por Thiago 86

Ter Abr 23, 2013 13:05
Funções
-
- Função do 2° Grau
por mimi2009 » Qua Jun 10, 2009 05:46
- 1 Respostas
- 2086 Exibições
- Última mensagem por Molina

Qua Jun 10, 2009 08:05
Funções
-
- Função do 2 grau...
por Fiel8 » Qua Jul 01, 2009 21:34
- 4 Respostas
- 3438 Exibições
- Última mensagem por Cleyson007

Qui Jul 02, 2009 16:16
Funções
-
- Função 1° grau
por DanielFerreira » Ter Set 22, 2009 14:14
- 2 Respostas
- 2136 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 19:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![\left[1, \right2] \left[1, \right2]](/latexrender/pictures/d4a647053823ba0ae6ce71898f4648b0.png) e negativa ou nula no intervalo
e negativa ou nula no intervalo ![\left[2 ,\right3] \left[2 ,\right3]](/latexrender/pictures/d85eb8f44ddacdfeecb8210f22cad768.png) .
.
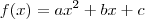 e determinar o produto ABC.
e determinar o produto ABC.

) e determinar o produto ABC.