 por rds0708 » Qua Mar 07, 2012 00:05
por rds0708 » Qua Mar 07, 2012 00:05
Boa noite.
Tenho lido livros sobre trigonometria e tentado me lembrar de coisas que estudei a uns 5 anos atrás. Sou programador e estou desenvolvendo objetos que se movimentam pela tela do computador. Tenho duas dúvidas que não sei mais como posso fazer para tentar a resolução e gostaria muito de uma ajuda:
[Dúvida 1]: Em um trinângulo reto, tenho tentado achar um ângulo alpha (um dos outros dois ângulos) utilizando as funções trigonométricas. Pelo que eu entendi, utilizamos funções trigonométricas para várias coisas, dentre elas achar os outros dois ângulos internos do triângulo retângulo. Eu fiz o cálculo utilizando a tangente de um ângulo alpha, cateto oposto dividido pelo cateto adjacente. O resultado que tive, pelo que li, é o valor do ângulo que desejo em radianos. Quando faço a mudança de radianos para graus, tenho um resultado errado do ângulo que estou procurando. Não sei o que estou fazendo errado.
[Aplicação de dúvida 1]: Estou tentando aplicar isso numa situação onde, por exemplo, temos dois objetos num plano cartesiano. Estes objetos têm posições X e Y. Imagine um dos objetos numa coordenada (150, 120), e o outro em outra coordenada (250 , 230). Ambos objetos têm um ângulo ao qual ele estão com suas faces viradas. O que quero fazer é com que um destes objetos olhe para outro destes objetos. Daí, consegui ver que posso resolver este problema com funções trigonométricas... Mas não tenho obtido sucesso.
[Dúvida 2]: Este dúvida segue a aplicação da dúvida anterior. Eu gostaria de saber como posso resolver uma situação em que eu tenha um objeto em um plano com posições X, Y e um ângulo face, e gostaria de descobrir qual é a próxima posição X e Y (supondo que o objeto está em movimento) de acordo com seu ângulo face.
[Aplicação de dúvida 2]: Hmm... Não sei bem onde aplicar isso por enquanto, mas tudo no que pensei foi em um jogo de nave, tipo Asteroids. Você vira a nave para um local no mapa (seu ângulo face), e começa a acelerar a nava. Com tal cálculo, é possível dar a nave suas próximas posições seguintes. A aceleração não é um problema, pode-se utilizar o tempo decorrido para fazer a atualização da posição da nave.
[OBS]: Só tem um pequeno detalhe que eu tenho que notificar a quem queira me ajudar. O plano cartesiano em computadores é diferente. Onde Y é positivo para cima na matemática, na informática o Y é positivo para baixo. Além disso, o grau 0 (zero) começa do norte (de cima), e aumenta em sentido horário.
Bom, é isso. Acredito que minha dúvida possa ajudar alguns programadores que venham aqui e talvez até a alguns matemáticos, quem sabe. Espero que alguém possa me ajudar.
Até.
-
rds0708
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 06, 2012 23:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informática
- Andamento: formado
 por timoteo » Qua Mar 07, 2012 03:42
por timoteo » Qua Mar 07, 2012 03:42
ha um equivoco. quando vc encontra a razao entre os catetos, esse valor esta associado a um numero na tabua trigonometrica e esse valor esta relacionado mais diretamente com o valor em graus.ex: 0,57 = tg 30°.
pelo que entendi vc esta usando um triangulo retangulo onde em um angulo agudo esta uma figura1 e no outro a figura2. pelo meu entendimento vc deve encontrar uma funçao para girar a sua imagem sobre seu proprio eixo e para isso vc pode parametrizar as duas funçoes utilizando o tempo com paramentro. note que seus problemas envolvem funçoes com mais de uma sentença.
entao eu acho que vc deve estudar alem de trigonometria, funçoes com mais de uma sentença, parametrizaçao e matrizes.
espero ter ajudado
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por rds0708 » Qua Mar 07, 2012 05:03
por rds0708 » Qua Mar 07, 2012 05:03
timoteo escreveu:ha um equivoco. quando vc encontra a razao entre os catetos, esse valor esta associado a um numero na tabua trigonometrica e esse valor esta relacionado mais diretamente com o valor em graus.ex: 0,57 = tg 30°.
pelo que entendi vc esta usando um triangulo retangulo onde em um angulo agudo esta uma figura1 e no outro a figura2. pelo meu entendimento vc deve encontrar uma funçao para girar a sua imagem sobre seu proprio eixo e para isso vc pode parametrizar as duas funçoes utilizando o tempo com paramentro. note que seus problemas envolvem funçoes com mais de uma sentença.
entao eu acho que vc deve estudar alem de trigonometria, funçoes com mais de uma sentença, parametrizaçao e matrizes.
espero ter ajudado
Nossa. Então quer dizer que o resultado que sai com a razão da tangente de um ângulo é equivalente a um dos campos da tabela trigonométrica? Não sabia, obrigado por me notificar. Porém existe um problema aí, não tenho como fazer com que um programa reconheça esse valor e ele vá sozinho consultar uma tabela trigonométrica. E se eu tivesse de fazer isso, teria de criar uma tabela de parâmetros utilizando um banco de dados só para que o programa tenha que procurar o valor que foi encontrado em qualquer função trigonométrica. Isso iria complicar ainda mais a minha vida.
Será que não existe um outro jeito de encontrar um ângulo X em um triângulo reto onde eu só tenha as medidas dos catetos, da hipotenusa e o ângulo de 90 graus para trabalho?Com relação a funções de tempo e etc, isso não é problema para mim. Vamos pensar uma coisa juntos, a atualização de tela (e seus componentes como, imagens, objetos e etc) acontece em ciclos. Estes ciclos se repetem no tempo e em intervalos que o programador quiser. Eu tenho como programar um objeto para que ele somente se mova a cada 10 milisegundos , por exemplo. Para isso, este mesmo objeto verifica se 10 milisegundos ou mais foram passados e é aí então que ele realiza o cálculo de movimento. O problema está justamente aí no cálculo. Eu consegui uma vez realizar este cálculo seguinto um livro de programação de interfaces gráficas, onde a fórmula para encontrar a próxima posição X e a próxima Y é algo (se não me engano) assim:
Próxima posição X = cos (a * PI / 180)
Próxima posição Y = sen (a * PI / 180)Onde a é igual ao ângulo face do objeto (o ângulo em que o objeto está apontando a sua face).
Não sei se estas fórmulas estão corretas. Se não estiverem, por favor me falem e me indiquem um caminho. Se estas fórmulas estão realmente corretas (que segundo o livro que peguei aqui agora, ela está, mas não sei o motivo), eu gostaria que alguém me ensinasse a lógica disso aí, se não for pedir muito, é claro.
Até.
-
rds0708
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 06, 2012 23:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informática
- Andamento: formado
 por LuizAquino » Qua Mar 07, 2012 08:56
por LuizAquino » Qua Mar 07, 2012 08:56
rds0708 escreveu:[Dúvida 1]: Em um trinângulo reto, tenho tentado achar um ângulo alpha (um dos outros dois ângulos) utilizando as funções trigonométricas. Pelo que eu entendi, utilizamos funções trigonométricas para várias coisas, dentre elas achar os outros dois ângulos internos do triângulo retângulo. Eu fiz o cálculo utilizando a tangente de um ângulo alpha, cateto oposto dividido pelo cateto adjacente. O resultado que tive, pelo que li, é o valor do ângulo que desejo em radianos. Quando faço a mudança de radianos para graus, tenho um resultado errado do ângulo que estou procurando. Não sei o que estou fazendo errado.
rds0708 escreveu:Será que não existe um outro jeito de encontrar um ângulo X em um triângulo reto onde eu só tenha as medidas dos catetos, da hipotenusa e o ângulo de 90 graus para trabalho?
Suponha que o triângulo retângulo tenha catetos
b e
c. Além disso, suponha que o cateto
c seja oposto ao ângulo interno

desse triângulo.
Para calcular o ângulo

, basta usar a função arco-tangente (que é a função inversa da tangente). Ou seja, temos que:

Tipicamente, nas bibliotecas matemáticas de linguagens de programação, a função arco-tangente é dada por
atan. Além disso, essa função tipicamente retorna o ângulo em radianos. Consulte o manual de referência da linguagem que você está usando.
rds0708 escreveu:[Dúvida 2]: Este dúvida segue a aplicação da dúvida anterior. Eu gostaria de saber como posso resolver uma situação em que eu tenha um objeto em um plano com posições X, Y e um ângulo face, e gostaria de descobrir qual é a próxima posição X e Y (supondo que o objeto está em movimento) de acordo com seu ângulo face.
rds0708 escreveu:Com relação a funções de tempo e etc, isso não é problema para mim. Vamos pensar uma coisa juntos, a atualização de tela (e seus componentes como, imagens, objetos e etc) acontece em ciclos. Estes ciclos se repetem no tempo e em intervalos que o programador quiser. Eu tenho como programar um objeto para que ele somente se mova a cada 10 milisegundos , por exemplo. Para isso, este mesmo objeto verifica se 10 milisegundos ou mais foram passados e é aí então que ele realiza o cálculo de movimento. O problema está justamente aí no cálculo. Eu consegui uma vez realizar este cálculo seguinto um livro de programação de interfaces gráficas, onde a fórmula para encontrar a próxima posição X e a próxima Y é algo (se não me engano) assim:
Próxima posição X = cos (a * PI / 180)
Próxima posição Y = sen (a * PI / 180)
Onde a é igual ao ângulo face do objeto (o ângulo em que o objeto está apontando a sua face).
Não sei se estas fórmulas estão corretas. Se não estiverem, por favor me falem e me indiquem um caminho. Se estas fórmulas estão realmente corretas (que segundo o livro que peguei aqui agora, ela está, mas não sei o motivo), eu gostaria que alguém me ensinasse a lógica disso aí, se não for pedir muito, é claro.
Suponha que o objeto esteja na posição (x0, y0). Além disso, seja

o seu "ângulo face". Se você deseja deslocar-se seguindo a direção dada pelo "ângulo face", então as novas posições (x, y) serão dadas por:
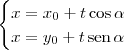
O parâmetro
t nas equações acima controla o tamanho do deslocamento. Por exemplo, se
t = 2, então o objeto irá se deslocar 2 unidades na direção dada pelo ângulo

. Lembrando que a "unidade" pode variar de acordo com o problema. Por exemplo, se 1 unidade for igual a 1 cm, então o deslocamento para
t = 2 seria de 2 cm.
Para entender o motivo dessas equações, vide a figura abaixo.
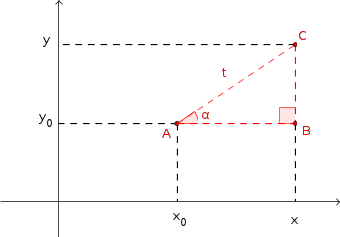
- figura.png (3.48 KiB) Exibido 6094 vezes
Analisando a figura, temos que:
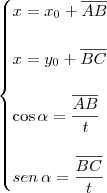
Usando essas quatro equações, podemos montar as equações para o deslocamento dadas anteriormente.
ObservaçãoÉ comum encontrar profissionais da área de Computação que "torcem o nariz" para a Matemática.
Mas veja como essa dúvida que você enviou ilustra a necessidade dos profissionais dessa área aprenderem os conteúdos de Matemática. Por exemplo, esse seu problema foi resolvido apenas aplicando conhecimentos de trigonometria.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rds0708 » Qua Mar 07, 2012 15:40
por rds0708 » Qua Mar 07, 2012 15:40
LuizAquino escreveu:Suponha que o triângulo retângulo tenha catetos b e c. Além disso, suponha que o cateto c seja oposto ao ângulo interno \alpha desse triângulo.
Para calcular o ângulo \alpha , basta usar a função arco-tangente (que é a função inversa da tangente). Ou seja, temos que:
\alpha = \textrm{arctg}\,\frac{c}{b}
Tipicamente, nas bibliotecas matemáticas de linguagens de programação, a função arco-tangente é dada por atan. Além disso, essa função tipicamente retorna o ângulo em radianos. Consulte o manual de referência da linguagem que você está usando.
Nossa! Não tinha a menor noção que utilizando a função inversa da tangente eu encontraria os radianos do ângulo que procuro. Obrigado pela dica!
LuizArquino escreveu:Suponha que o objeto esteja na posição (x0, y0). Além disso, seja \alpha o seu "ângulo face". Se você deseja deslocar-se seguindo a direção dada pelo "ângulo face", então as novas posições (x, y) serão dadas por:
\begin{cases} x = x_0 + t\cos \alpha \\ x = y_0 + t\,\textrm{sen}\, \alpha \end{cases}
O parâmetro t nas equações acima controla o tamanho do deslocamento. Por exemplo, se t = 2, então o objeto irá se deslocar 2 unidades na direção dada pelo ângulo \alpha . Lembrando que a "unidade" pode variar de acordo com o problema. Por exemplo, se 1 unidade for igual a 1 cm, então o deslocamento para t = 2 seria de 2 cm.
Pela figura, faz muito sentido, aliás, faz todo sentido.
Me confirma uma coisa para ver se eu entendi, você disse que a próxima posição X, é igual a posição X anterior, mais a distância AB, e que a próxima posição Y, é igual a posição Y anterior, mais a distância BC, correto? Outra coisa, eu utilizando seno e cosseno de alpha, eu tenho como encontrar todas as distâncias do triângulo, não é?
A fórmula final ficou desse jeito, mas não sou matemático, devo multiplicar o tamanho do deslocamento (t) pelo seno ou cosseno de alpha?LuizArquino escreveu:Mas veja como essa dúvida que você enviou ilustra a necessidade dos profissionais dessa área aprenderem os conteúdos de Matemática. Por exemplo, esse seu problema foi resolvido apenas aplicando conhecimentos de trigonometria.
Não foi a toa que recorri a estudar trigonometria. Fazia anos que eu não pegava em livros sobre o assunto e quando, de primeira vez, pensei em como resolveria o problema, logo desenhei e encontrei um triângulo retângulo. Atualmente faço um estudo aprofundado em interfaces gráficas e a manutenção e modelagem top-down de bancos de dados (que na minha opinião, é uma coisa linda!). Sou mais um programador (e pessoa) que quer deixar bem claro a todo mundo, matemática
É essencial em qualquer situação do nosso dia-a-dia. Nós sempre estamos usando matemática, mesmo que seja de um conteúdo mais "bobo" até um mais "pesadinho". De fato, não tenho estudado matemática já faz um tempo. Nossas vidas hoje em dia estão cada vez mais corridas. Temos prazos e etc... Enfim, não quero deixar de concordar que vez ou outra a gente tem que tirar o carro da garagem e andar com ele um pouco. E devido a falta de uso, provavelmente precisaremos da ajuda de um profissional da área, e de um professor que tenha o jeito de nos ensinar.

Até.
-
rds0708
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 06, 2012 23:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informática
- Andamento: formado
 por LuizAquino » Qua Mar 07, 2012 20:05
por LuizAquino » Qua Mar 07, 2012 20:05
rds0708 escreveu:Me confirma uma coisa para ver se eu entendi, você disse que a próxima posição X, é igual a posição X anterior, mais a distância AB, e que a próxima posição Y, é igual a posição Y anterior, mais a distância BC, correto?
Correto.
rds0708 escreveu:Outra coisa, eu utilizando seno e cosseno de alpha, eu tenho como encontrar todas as distâncias do triângulo, não é?
Eu presumo que você queira dizer "lados do triângulo" ao invés de "distâncias do triângulo".
Se for conhecido o ângulo alfa e qualquer um dos lados do triângulo retângulo, então é possível determinar os outros dois lados.
Se for conhecido
apenas os ângulos internos de um triângulo retângulo, então não é possível determinar os seus lados.
No seu caso, você conhece o ângulo e a hipotenusa (que corresponde ao tamanho do deslocamento t escolhido). Dessa forma, você pode determinar os catetos desse triângulo.
rds0708 escreveu:A fórmula final ficou desse jeito, mas não sou matemático, devo multiplicar o tamanho do deslocamento (t) pelo seno ou cosseno de alpha?
Você não deve dizer "pelo seno
ou pelo cosseno". O correto seria dizer "pelo seno
e pelo cosseno".
Do jeito que você escreveu, a pessoa poderia, por exemplo, multiplicar t apenas pelo seno de alfa. Mas esse não é o caso.
Você deve multiplicar o valor de t tanto pelo seno quanto pelo cosseno de alfa.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rds0708 » Qua Mar 07, 2012 21:54
por rds0708 » Qua Mar 07, 2012 21:54
LuizAquino escreveu:rds0708 escreveu:Me confirma uma coisa para ver se eu entendi, você disse que a próxima posição X, é igual a posição X anterior, mais a distância AB, e que a próxima posição Y, é igual a posição Y anterior, mais a distância BC, correto?
Correto.
rds0708 escreveu:Outra coisa, eu utilizando seno e cosseno de alpha, eu tenho como encontrar todas as distâncias do triângulo, não é?
Eu presumo que você queira dizer "lados do triângulo" ao invés de "distâncias do triângulo".
Se for conhecido o ângulo alfa e qualquer um dos lados do triângulo retângulo, então é possível determinar os outros dois lados.
Se for conhecido
apenas os ângulos internos de um triângulo retângulo, então não é possível determinar os seus lados.
No seu caso, você conhece o ângulo e a hipotenusa (que corresponde ao tamanho do deslocamento t escolhido). Dessa forma, você pode determinar os catetos desse triângulo.
rds0708 escreveu:A fórmula final ficou desse jeito, mas não sou matemático, devo multiplicar o tamanho do deslocamento (t) pelo seno ou cosseno de alpha?
Você não deve dizer "pelo seno
ou pelo cosseno". O correto seria dizer "pelo seno
e pelo cosseno".
Do jeito que você escreveu, a pessoa poderia, por exemplo, multiplicar t apenas pelo seno de alfa. Mas esse não é o caso.
Você deve multiplicar o valor de t tanto pelo seno quanto pelo cosseno de alfa.
Perfeito. Entendi tudo o que você me disse e estou totalmente grato pela sua ajuda! Você me ajudou com calma e de forma didática! Vou indicar esse fórum para meus colegas e tenho certeza de que alguns adorarão dar uma passada por aqui de vez em quando.
No momento eu estou refazendo meu framework de interfaces para começar novos testes e aplicar tudo o que você me ensinou aqui. Mal posso esperar! Assim que eu fizer os testes eu venho aqui dar um feedback para fechar o tópico com conteúdo e resolução final.
Mais uma vez, obrigado!
Até.
-
rds0708
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 06, 2012 23:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informática
- Andamento: formado
 por rds0708 » Seg Mar 12, 2012 16:58
por rds0708 » Seg Mar 12, 2012 16:58
Olá.
Bom pessoal, só estou passando aqui para agradecer pela ajuda e dizer que realmente foi útil e solucionou meu problema. Tenho tido problemas com meu framework de interfaces, mas não por causa da matemática e sim por causa da falta de conhecimento em certos pontos da minha área de programação (em maior foco, a minha linguagem, Java). Algumas coisas são mais complicadas do que pensei que seriam. Enfim, eu não estou aqui para falar de programação, este é um fórum de matemática. Eu fiz todos os cálculos no papel e tudo resultou em algo totalmente perfeito. O tempo de movimento de interfaces foi feito com base no ciclo da aplicação. Pude movimentar qualquer objeto em qualquer velocidade impondo regras de que tal objeto deve mover-se a cada X milisegundos. O olho humano é redondamente enganado tendo a ilusão de que o objeto está se movendo mais rápido ou mais devagar. Utilizando o cálculo trigonométrico pude mover livremente objetos de interface em um plano bidimensional.
Nada está completo ainda, mas as coisas estão funcionando aos poucos. Gostaria de poder mostrar a vocês o que estou fazendo, mas no momento ando muito ocupado e muito estressado até para fazer isso funcionar do jeito correto. Quero agradecer novamente pela ajuda: Obrigado!

Até.
-
rds0708
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Ter Mar 06, 2012 23:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Funções]Plano Cartesiano
 por ti123 » Qui Out 08, 2020 09:36
por ti123 » Qui Out 08, 2020 09:36
- 2 Respostas
- 7362 Exibições
- Última mensagem por DanielFerreira

Dom Out 25, 2020 16:06
Funções
-
- Plano cartesiano
 por Jaison Werner » Sex Abr 23, 2010 21:06
por Jaison Werner » Sex Abr 23, 2010 21:06
- 1 Respostas
- 2619 Exibições
- Última mensagem por Molina

Sáb Abr 24, 2010 13:06
Geometria Analítica
-
- Plano cartesiano
por Jaison Werner » Ter Abr 27, 2010 18:57
- 1 Respostas
- 1990 Exibições
- Última mensagem por Neperiano

Ter Set 27, 2011 19:53
Geometria Analítica
-
- Plano Cartesiano Bidimensional
por vanessafey » Dom Jul 10, 2011 14:24
- 1 Respostas
- 2327 Exibições
- Última mensagem por MarceloFantini

Seg Jul 11, 2011 03:20
Geometria Analítica
-
- Triângulo no plano cartesiano
por Evelyn 1 » Ter Jan 17, 2012 20:38
- 1 Respostas
- 2085 Exibições
- Última mensagem por Arkanus Darondra

Ter Jan 17, 2012 21:18
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 desse triângulo.
desse triângulo.
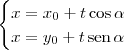
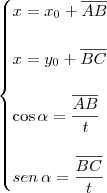


 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: