 por marcia_abreu » Sáb Fev 25, 2012 18:39
por marcia_abreu » Sáb Fev 25, 2012 18:39
Por favor, preciso de ajuda com um problema de análise combinatóri?a. O problema é: Uma organização dispõe de 8 economistas e 5 engenheiros?. De quantos modos podemos formar uma comissão com 6 membros, se cada comissão deve ter, no mínimo, 3 engenheiros?? Resolvi assim: dividi a comissão de 6 membros em duas comissões de 3 membros cada uma; a primeira, uma comissão de 3 engenheiros e a segunda, uma comissão que pode ser formada com 8 economistas e os 2 engenheiros que não entraram na primeira comissão e depois multiplique?i uma pela outra para formar o número de comissões possíveis de 6 membros. Assim, na primeira comissão, são 5 engenheiros ocupando 3 lugares distintos, dividido pelo número de combinações totais de 3 engenheiros distintos, para que assim a ordem de escolha dos membros não faça diferença na comissão. Depois, a mesma coisa com os outros 10 membros (8 economistas?+2 engenheiros sobrando). A fórmula fica assim: (5x4x3/3x2) x (10x9x8/3x2?) = 1200. Mas o gabarito dá 708. Alguém pode ajudar? Grata, Marcia
-
marcia_abreu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 25, 2012 18:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História da Arte
- Andamento: formado
 por fraol » Sáb Fev 25, 2012 19:31
por fraol » Sáb Fev 25, 2012 19:31
A abordagem para resolver esse problema pode ser assim, por exemplo:
Com no mínimo 3 engenheiros em cada comissão de 6 membros, você pode ter as seguintes situações:
Uma comissão com 3 engenheiros escolhidos entre 5 e 3 economistas escolhidos entre 8:
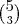
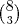
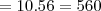
Ou
Uma comissão com 4 engenheiros escolhidos entre 5 e 2 economistas escolhidos entre 8:


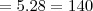
Ou
Uma comissão com 5 engenheiros escolhidos entre 5 e 1 economista escolhido entre 8:
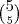
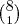
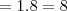
Então somando
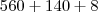
você obtém
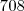
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por marcia_abreu » Sáb Fev 25, 2012 19:44
por marcia_abreu » Sáb Fev 25, 2012 19:44
Fraol, agradeço a sua ajuda. Cheguei a pensar em seguir por esse caminho tb, mas não o fiz, dá pra notar, né? Mas por favor, me diga o que há de errado com o meu raciocínio inicial. Pq a minha abordagem anterior não chega no mesmo resultado? Eu ainda não entendi qual o meu erro... Obrigada mais uma vez, Márcia
fraol escreveu:A abordagem para resolver esse problema pode ser assim, por exemplo:
Com no mínimo 3 engenheiros em cada comissão de 6 membros, você pode ter as seguintes situações:
Uma comissão com 3 engenheiros escolhidos entre 5 e 3 economistas escolhidos entre 8:
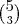
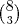
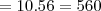
Ou
Uma comissão com 4 engenheiros escolhidos entre 5 e 2 economistas escolhidos entre 8:


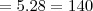
Ou
Uma comissão com 5 engenheiros escolhidos entre 5 e 1 economista escolhido entre 8:
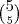
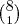
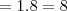
Então somando
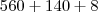
você obtém
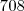
.
-
marcia_abreu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 25, 2012 18:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História da Arte
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16391 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12560 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8482 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7935 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6631 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



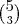
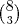
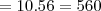


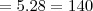
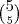
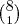
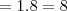
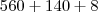 você obtém
você obtém 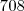 .
.
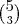
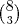


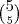
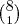
você obtém
.






