 por apaula » Sex Fev 17, 2012 15:48
por apaula » Sex Fev 17, 2012 15:48
Não existem soluções racionais pra a equação
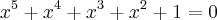
-----------
Fazendo a demonstração por absurdo foi admitida a fração

irredutível q satisfaz a equação
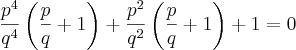
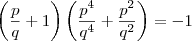
assim:
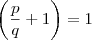
e

ou
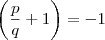
e
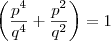
Tomando
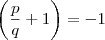
temos que

e ,portaanto, fração não é irreduível (
é importante dizer q a fração não é irredutível?)
e depois?
-
apaula
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Fev 17, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bachrelado em Ciência e Tecnologia
- Andamento: cursando
 por MarceloFantini » Sáb Fev 18, 2012 00:23
por MarceloFantini » Sáb Fev 18, 2012 00:23
Se você tem o produto de dois números
racionais que tem valor -1, não é verdade que um deles precisa ser um e outro precisa ser -1. Como um contra-exemplo simples, tome

e

de forma que

mas

e

. É importante lembrar que

tem de
necessariamente ser positivo, pois é soma de dois quadrados e isto jamais será negativo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por apaula » Sáb Fev 18, 2012 21:30
por apaula » Sáb Fev 18, 2012 21:30
ainda assim não consegui resolver.
algume ajuda?
-
apaula
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Fev 17, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bachrelado em Ciência e Tecnologia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DEMONSTRAÇÃO POR REDUÇÃO AO ABSURDO
por washington_araujo » Ter Jun 26, 2012 10:28
- 5 Respostas
- 3556 Exibições
- Última mensagem por washington_araujo

Sex Jun 29, 2012 11:33
Álgebra Elementar
-
- PROVAR POR ABSURDO!!!!
por Rose » Sex Set 26, 2008 19:21
- 2 Respostas
- 3642 Exibições
- Última mensagem por admin

Ter Set 30, 2008 17:56
Geometria Plana
-
- Absurdo Matemático
 por PedroSantos » Sáb Jan 15, 2011 19:18
por PedroSantos » Sáb Jan 15, 2011 19:18
- 2 Respostas
- 1904 Exibições
- Última mensagem por PedroSantos

Dom Jan 16, 2011 19:42
Álgebra Elementar
-
- Deonstração por absurdo
por apaula » Sex Fev 17, 2012 12:04
- 2 Respostas
- 3840 Exibições
- Última mensagem por lua_guyl

Ter Jun 30, 2015 13:01
Álgebra Elementar
-
- Prova por redução ao absurdo
por Aliocha Karamazov » Sex Jun 10, 2011 21:34
- 1 Respostas
- 3309 Exibições
- Última mensagem por Guill

Sáb Jul 23, 2011 22:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
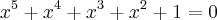
 irredutível q satisfaz a equação
irredutível q satisfaz a equação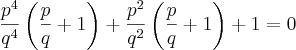
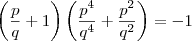
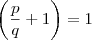 e
e 
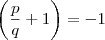 e
e 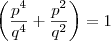
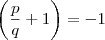
 e ,portaanto, fração não é irreduível (é importante dizer q a fração não é irredutível?)
e ,portaanto, fração não é irreduível (é importante dizer q a fração não é irredutível?)
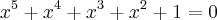
 irredutível q satisfaz a equação
irredutível q satisfaz a equação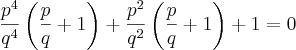
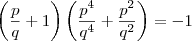
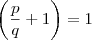 e
e 
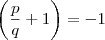 e
e 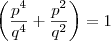
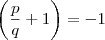
 e ,portaanto, fração não é irreduível (é importante dizer q a fração não é irredutível?)
e ,portaanto, fração não é irreduível (é importante dizer q a fração não é irredutível?)
 e
e  de forma que
de forma que  mas
mas  e
e  . É importante lembrar que
. É importante lembrar que  tem de necessariamente ser positivo, pois é soma de dois quadrados e isto jamais será negativo.
tem de necessariamente ser positivo, pois é soma de dois quadrados e isto jamais será negativo.



