(16:55:22) Joaozulu: Não consigo concluir a seguinte questão: 27!=n.10^p.
(16:57:17) Joaozulu: Minha tentativa: 27.26!=n.10^p => 26!=10^p => log 26!=p ... Faz sentido?





Joaozulu escreveu:(UNB-DF) Admita que 27!=n.10^p, em que n e p são números naturais e n não é múltiplo de 10. Calcule o valor de p.
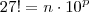
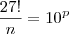
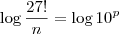
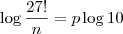
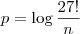
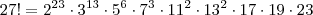
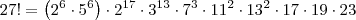
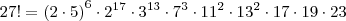
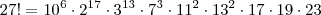
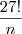 que aparece dentro do logaritmo (na base 10) deve ser uma potência de 10. Para que isso aconteça, devemos ter:
que aparece dentro do logaritmo (na base 10) deve ser uma potência de 10. Para que isso aconteça, devemos ter: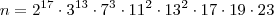

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



