



Renato_RJ escreveu:Boa noite !!
O log f vem do fato do cara que resolveu a conta ter feito a integral do lado esquerdo da igualdade, em 7, em relação a f e do lado direito em relação a x, veja:
Tranquilo ?

 e eu não lembro a demonstração dela.. rssss.....
e eu não lembro a demonstração dela.. rssss.....



giboia90 escreveu:poderia resolve- la de mode detalhada.
giboia90 escreveu:e como o d multiplica o log de F. e onde sai esse c.
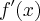 , sendo que após todas as simplificações nós obtemos no final do passo 5) que essa expressão é equivalente a
, sendo que após todas as simplificações nós obtemos no final do passo 5) que essa expressão é equivalente a 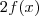 .
.

![\left[\ln f(x) - 2x\right]^\prime \left[\ln f(x) - 2x\right]^\prime](/latexrender/pictures/73262f32278f25c79d392fac41aea1f0.png)
![\left[\ln f(x) - 2x\right]^\prime = 0 \left[\ln f(x) - 2x\right]^\prime = 0](/latexrender/pictures/a4f68d7a3f1954d16d6eadcaaefc8d32.png)
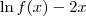 é igual a uma constante. Vamos chamar essa constante de c. Podemos então escrever que:
é igual a uma constante. Vamos chamar essa constante de c. Podemos então escrever que:

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

