Sequência - equação de diferença logística.

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Sequência - equação de diferença logística.

Regras do fórum
Responder

Sequência - equação de diferença logística.

Mensagempor Diego Luiz » Ter Dez 06, 2011 17:41

Boa tarde pessoal, tenho um projeto aplicado pra desenvolver, e gostaria de alguma ajuda pra entender melhor.

O enunciado desse projeto aplicado esta na pagina 652 do Stewart volume 2, o assunto é sequencias.

Uma sequência q aparece em ecologia é definida pela equação de diferença logística:

{p}_{n+1} = k{p}_{n}(1 - {p}_{n})

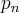onde {p}_{n} mede o tamanho da população da n-ésima geração de uma unica especie para manter os números manejéveis, 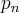{p}_{n} é uma fração do tamanho máximo da população, e assim 0\leq{p}_{n}\leq1.

Um ecologista está interessado em prever o tamanho da população com o passar do tempo e faz as perguntas: ela estabilizará em um valor-limite? Ela mudará de uma maneira cíclica? Ou ela exibirá comportamento aléatório?

Eu tenho que escrever um programa pra calcuar os n primeiros dessa sequencia começando com uma população inicial 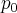{p}_{0}, onde 0\prec{p}_{0}\prec1.

Inicialmente eu gostaria de ajuda para entender melhor essa sequencia. e entender tambem sobre as perguntas do ecologistas.

desde já agradeço.
Diego Luiz
Novo Usuário
Novo Usuário
 
Mensagens: 1
Registrado em: Ter Dez 06, 2011 17:01
Formação Escolar: GRADUAÇÃO
Área/Curso: Licenciatura em Computação
Andamento: cursando
Voltar ao topo
Responder

Voltar para Sequências

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum