Bom dia tentei de diversas formas resolver essa equaçao mais nda da certo por tanto gostaria da ajuda de vcs
Encontrar a equaçao geral do plano que pertence ao ponto M (123) e é perpendicular a reta R de equaçao X=(410)+N.(111)
GRATO



ilariun escreveu:Encontrar a equaçao geral do plano que pertence ao ponto M (123) e é perpendicular a reta R de equaçao X=(410)+N.(111)
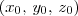 e tem vetor normal
e tem vetor normal  , é dada por:
, é dada por: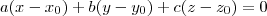
 é o vetor normal do plano e
é o vetor normal do plano e 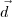 é o vetor diretor da reta, então
é o vetor diretor da reta, então 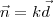 , para algum escalar k.
, para algum escalar k. .
. .
.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

