 por Jota17 » Sáb Nov 05, 2011 22:40
por Jota17 » Sáb Nov 05, 2011 22:40
Estou com duvida nessa questão de derivar e simplificar:
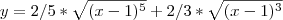
O gabarito é
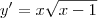
.
Eu fiz separando a equação total em 2 partes, parte A, e parte B. Onde eu derivo e simplifico ambas, e depois junto elas.
Juntando as duas:
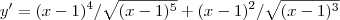
Tirei o MMC, e que eu acho que é nisso que eu estou errando e cheguei nisso:
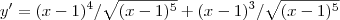
Não consigo chegar na resposta, alguem pode me dar alguma dica? Eu fiz algo errado?
-
Jota17
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 05, 2011 21:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Ter Nov 08, 2011 00:22
por LuizAquino » Ter Nov 08, 2011 00:22
Jota17 escreveu:Tirei o MMC, e que eu acho que é nisso que eu estou errando e cheguei nisso:
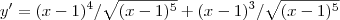
Não consigo chegar na resposta, alguem pode me dar alguma dica? Eu fiz algo errado?
Note que:
^3 = x(x-1)^3 (x-1)^4 + (x-1)^3 = [(x-1)+1](x-1)^3 = x(x-1)^3](/latexrender/pictures/f11926b10a481413e9bd807cf656bc5d.png)
Além disso, temos também que:
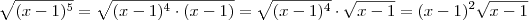
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivar
por fcosta » Ter Nov 29, 2016 12:32
- 4 Respostas
- 6126 Exibições
- Última mensagem por fcosta

Qua Nov 30, 2016 18:54
Cálculo: Limites, Derivadas e Integrais
-
- DERIVAR ou INTEGRAR
por DESESPERADO » Qui Nov 11, 2010 14:14
- 15 Respostas
- 13396 Exibições
- Última mensagem por andrefahl

Sex Nov 12, 2010 17:45
Cálculo: Limites, Derivadas e Integrais
-
- derivar a função
por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
- 3 Respostas
- 3847 Exibições
- Última mensagem por SILMARAKNETSCH

Qua Nov 14, 2012 21:57
Funções
-
- Derivar f(X) = (x²+7)²Raiz(1-x)
por Henrique Webber » Sex Nov 22, 2013 20:02
- 0 Respostas
- 1015 Exibições
- Última mensagem por Henrique Webber

Sex Nov 22, 2013 20:02
Cálculo: Limites, Derivadas e Integrais
-
- Derivar uma função
por rcs01 » Qui Abr 30, 2015 09:48
- 0 Respostas
- 2342 Exibições
- Última mensagem por rcs01

Qui Abr 30, 2015 09:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
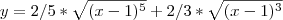
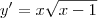 .
.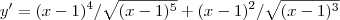
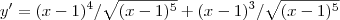


^3 = x(x-1)^3 (x-1)^4 + (x-1)^3 = [(x-1)+1](x-1)^3 = x(x-1)^3](/latexrender/pictures/f11926b10a481413e9bd807cf656bc5d.png)
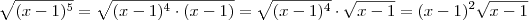


 .
.



