 por Arth » Sex Nov 04, 2011 09:43
por Arth » Sex Nov 04, 2011 09:43
Bom dia !
Estou trancado nessa questão, preciso muito saber como faz pois provavelmente irá cair na prova de hoje !
Depois de fazer a integração por partes não estou achando mais o que fazer, pois sempre que substituo o intervalo ele vai a 0.
Segue a questão:

Sabendo que
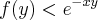
, use a integração por partes para mostrar que:

Qualquer coisa já me ajuda !
Grato.
-
Arth
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Nov 04, 2011 09:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral Imprópria
por CrazzyVi » Seg Set 27, 2010 17:13
- 5 Respostas
- 7249 Exibições
- Última mensagem por menino de ouro

Qui Jan 24, 2013 13:43
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por menino de ouro » Dom Jan 13, 2013 17:04
- 3 Respostas
- 2453 Exibições
- Última mensagem por thejotta

Seg Jan 14, 2013 00:11
Cálculo: Limites, Derivadas e Integrais
-
- Integral Imprópria
por Man Utd » Sex Ago 09, 2013 16:09
- 0 Respostas
- 1244 Exibições
- Última mensagem por Man Utd

Sex Ago 09, 2013 16:09
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por vanu » Qui Dez 12, 2013 20:05
- 1 Respostas
- 1410 Exibições
- Última mensagem por Man Utd

Sex Dez 13, 2013 11:22
Cálculo: Limites, Derivadas e Integrais
-
- Integral impropria
por isabelrebelo » Qui Abr 23, 2015 17:24
- 0 Respostas
- 1572 Exibições
- Última mensagem por isabelrebelo

Qui Abr 23, 2015 17:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

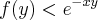 , use a integração por partes para mostrar que:
, use a integração por partes para mostrar que:


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.