camposhj escreveu:Mas e os demais pontos B,C e D eu escolho qquer ponto.
É claro que não! Os outros vértices você deve determinar levando em consideração que o losango que
escolhemos construir tem lados medindo 2 u. c. e ângulos internos dados por 60° e 120°.
Por exemplo, seja B = (k, m). Note que podemos escrever que:
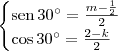
Lembrando-se que

e

, obtemos que
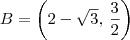
.
Utilizando um procedimento análogo você pode determinar os outros vértices.
Mas lembre-se que algumas coordenadas dos outros vértices você não precisa mais calcular. Por exemplo, note que
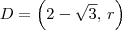
(pois D na construção tem a mesma coordenada x do que B) e que
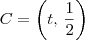
(pois C na construção tem a mesma coordenada y do que A). Portanto, você precisa apenas determinar o valor de
r e
t.


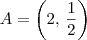 e os seus ângulos internos são 60° e 120° (na figura está ilustrado apenas metade de cada um deles). A partir disso você pode encontrar os outros vértices e calcular os produtos escalares desejados.
e os seus ângulos internos são 60° e 120° (na figura está ilustrado apenas metade de cada um deles). A partir disso você pode encontrar os outros vértices e calcular os produtos escalares desejados.
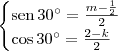
 e
e  , obtemos que
, obtemos que 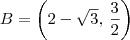 .
.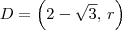 (pois D na construção tem a mesma coordenada x do que B) e que
(pois D na construção tem a mesma coordenada x do que B) e que 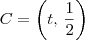 (pois C na construção tem a mesma coordenada y do que A). Portanto, você precisa apenas determinar o valor de
(pois C na construção tem a mesma coordenada y do que A). Portanto, você precisa apenas determinar o valor de 