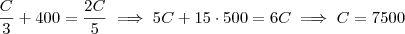por mara alves » Sáb Set 17, 2011 13:08
por mara alves » Sáb Set 17, 2011 13:08
estou tentando ajudar meu filho mas o resultado que eu consigo é diferente do que a prof. passou em sala?
um reservatório estava totalmente cheio de água , esvaziou-se 1/3 da capacidade desse reservatório e a seguir foram retirados 400 litros de agua o que restou corresponde a 3/5 da capacidade, quantos litros tem o reservatório, para mim tem 6.000 litros?
-
mara alves
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Set 17, 2011 12:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso de magistério
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação de 2° grau, envolvendo problemas - exercicios
por Felipe_95 » Seg Out 04, 2010 20:49
- 4 Respostas
- 3211 Exibições
- Última mensagem por DanielRJ

Seg Out 04, 2010 22:40
Sistemas de Equações
-
- Problemas equação 1° grau, dúvida.
por Clairelz12 » Sáb Ago 29, 2009 03:44
- 4 Respostas
- 7452 Exibições
- Última mensagem por Elcioschin

Sáb Ago 29, 2009 19:18
Álgebra Elementar
-
- Problemas de equação e sistemas de 1º grau
por gigante2010 » Dom Out 17, 2010 15:22
- 3 Respostas
- 4216 Exibições
- Última mensagem por MarceloFantini

Dom Out 17, 2010 23:00
Tópicos sem Interação (leia as regras)
-
- Problemas de equação do primeiro grau.
por Andrewo » Seg Fev 20, 2012 08:55
- 2 Respostas
- 5677 Exibições
- Última mensagem por Andrewo

Seg Fev 20, 2012 11:35
Sistemas de Equações
-
- Problemas de equação do primeiro grau.
por Andrewo » Qui Fev 23, 2012 18:00
- 3 Respostas
- 4529 Exibições
- Última mensagem por LuizAquino

Sex Fev 24, 2012 10:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.