 por matway » Sáb Set 10, 2011 18:24
por matway » Sáb Set 10, 2011 18:24
Boa tarde
Como resolver o seguinte problema: Usando as razões trigonométricas num triângulo retângulo, determine as medidas x e y indicadas na figura, dadas em centímetros. Em seguida, determine a área do losângo ABCD.

Uploaded with
ImageShack.us Obrigada
-
matway
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Set 04, 2011 17:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estudos Sociais
- Andamento: formado
 por MarceloFantini » Sáb Set 10, 2011 19:30
por MarceloFantini » Sáb Set 10, 2011 19:30
Você tentou aplicar as razões trigonométricas, ou seja, seno e cosseno?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matway » Sáb Set 10, 2011 20:34
por matway » Sáb Set 10, 2011 20:34
Sim, chego ao resultado de x=20 e y=20. Mas o gabarito diz que a área é = 1385,64cm2. Gostaria de saber como?
Obrigada
-
matway
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Set 04, 2011 17:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estudos Sociais
- Andamento: formado
 por MarceloFantini » Sáb Set 10, 2011 20:39
por MarceloFantini » Sáb Set 10, 2011 20:39
Seu resultado está parcialmente errado. Note que

mas
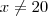
e sim
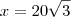
. A área total será 4 vezes a área de um triângulo, logo
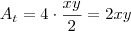
. Perceba que sua construção é impossível pois se x e y fossem iguais teríamos um triângulo isósceles, e como é retângulo também teríamos que os ângulos seriam de 45° e não 30° e 60° como são na realidade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por matway » Sáb Set 10, 2011 21:17
por matway » Sáb Set 10, 2011 21:17
Agradeço muito sua ajuda Marcelo, me ajudou bastante sua explicação.
Abraços
-
matway
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Set 04, 2011 17:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estudos Sociais
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4412 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2129 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2898 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 4162 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 mas
mas 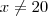 e sim
e sim 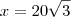 . A área total será 4 vezes a área de um triângulo, logo
. A área total será 4 vezes a área de um triângulo, logo 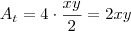 . Perceba que sua construção é impossível pois se x e y fossem iguais teríamos um triângulo isósceles, e como é retângulo também teríamos que os ângulos seriam de 45° e não 30° e 60° como são na realidade.
. Perceba que sua construção é impossível pois se x e y fossem iguais teríamos um triângulo isósceles, e como é retângulo também teríamos que os ângulos seriam de 45° e não 30° e 60° como são na realidade.


 .
.
 :
: