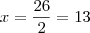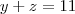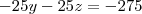por Pstefani » Dom Set 04, 2011 23:52
por Pstefani » Dom Set 04, 2011 23:52
Boa Noite Amigos.
É a minha primeira dúvida aqui neste fórum, espero poder compartilhar experiências juntos, bom vamos ao que enteressa:
Um posto presta serviço para os seus clientes, atendendo 3 tipo de automóveis: carro de passeio, camionete e caminhões. O valor cobrado para o carro de passeio é R$17,00, camionetes R$25,00 e caminhões R$30,00. Em um final de semana foram atendidos 24 veículos e o valor arrecadado foi de R$506,00. Sabe-se que o numero de carros de passeio superou os demais em duas unidades. Resolva o sistema correspondente:
X+Y+Z=24
17X+25Y+30Z=506
x=2+y+z
Acho que montei o sistema corretamente? Tranquei nesta parte, não sei como montar o resto da equação, se alguém puder me dar uma luz,não quero a resposta mas se puderem me dar uma dica fico muito agradecido.
-
Pstefani
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Set 04, 2011 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ti
- Andamento: cursando
 por Caradoc » Seg Set 05, 2011 09:18
por Caradoc » Seg Set 05, 2011 09:18
Está correto.
Você tem agora 3 equações para 3 incógnitas, ou seja, você vai conseguir resolver o sistema.
Somando a Eq1 + Eq3 você já descobre o valor de x.
Depois você pode substituir o valor encontrado nas Eq1 e Eq2, sobrando só 2 equações contendo y e z. A partir daí você resolve pra y e z também.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Pstefani » Seg Set 05, 2011 14:47
por Pstefani » Seg Set 05, 2011 14:47
Muito Obrigado pela resposta, mas to com dificuldades ainda,
X+Y+Z=24
x=2+y+z
2X + 2 + 2y + 2z=24
Fica desta forma? estou no caminho certo?
Desde já agradeço.
-
Pstefani
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Set 04, 2011 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ti
- Andamento: cursando
 por Caradoc » Seg Set 05, 2011 22:56
por Caradoc » Seg Set 05, 2011 22:56
Você tem que somar lado esquerdo de uma equação com o lado esquerdo da outra, o mesmo com o lado direito.


Aí você pode cancelar z e y que estão somando dos dois lados, ficando:

Daí você conclui que:
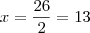
Agora você pode substituir x=13 nas 2 primeiras equações e usar método da soma para resolver o resto.
Só lembrando que o interessante no método da soma é você multiplicar uma equação inteira por um número de forma que ao somar com a outra, você consiga eliminar uma variável.
Por exemplo, depois de substituir x=13 na primeira equação ficamos com:
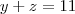
Agora você deve multiplicar essa equação por algo lhe perminta cancelar uma variável na soma. Por exemplo, multiplicando tudo por -25.
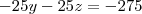
Note que ao somar com a segunda equação a variável y vai sumir, permitindo que você encontre z.
Tente agora
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Pstefani » Ter Set 06, 2011 00:23
por Pstefani » Ter Set 06, 2011 00:23
Muito Obrigado mesmo pela ajuda!!
Consegui entender bem a parte da montagem, porém o meu resultado não bate com o gabarito, veja só:
y+z=11 (-25)
25y+30z=506
-25z=-275
30z = 506
5z=231
z=231/5
z=46,20
Onde será que está errado?
Obrigado
-
Pstefani
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Set 04, 2011 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ti
- Andamento: cursando
 por Caradoc » Ter Set 06, 2011 09:06
por Caradoc » Ter Set 06, 2011 09:06
Você só se esqueceu de substituir o x = 13 na segunda equação.
Seria 17*13 + 25y +30z = 506
Ficando:
25y + 30z = 285
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Pstefani » Ter Set 06, 2011 09:47
por Pstefani » Ter Set 06, 2011 09:47
Caradoc, feito!!!
Muito Obrigado mesmo pela ajuda.
-
Pstefani
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Set 04, 2011 23:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ti
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Método de Jacob] - Sistemas Lineares
por Bruhh » Seg Mar 19, 2012 20:34
- 0 Respostas
- 886 Exibições
- Última mensagem por Bruhh

Seg Mar 19, 2012 20:34
Sistemas de Equações
-
- [Sistemas Lineares] Precisão do Método de Gauss-Seidel
por VFernandes » Qui Out 06, 2011 13:50
- 0 Respostas
- 1115 Exibições
- Última mensagem por VFernandes

Qui Out 06, 2011 13:50
Sistemas de Equações
-
- Matrizes inversas metodo adição
por watson » Qua Fev 22, 2012 16:33
- 4 Respostas
- 3182 Exibições
- Última mensagem por LuizAquino

Qua Fev 22, 2012 22:44
Geometria Analítica
-
- Sistemas Lineares
por Cleyson007 » Sáb Mai 03, 2008 01:50
- 3 Respostas
- 7031 Exibições
- Última mensagem por admin

Dom Mai 04, 2008 13:51
Sistemas de Equações
-
- Sistemas Lineares
por gustavowelp » Sáb Jun 26, 2010 17:05
- 3 Respostas
- 7789 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 09:09
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.