log (x-2), na base 2, + log x, na base 2, = 3
eu fiz da seguinte forma:
como os logaritmos são da mesma base, eu resolvi o logaritmando:
log (x-2), na base 2, + log x, na base 2 = (x-2).(x) --> x² -2x =3 --> x² -2x -3 = 0 --> 2+4/2 = 3 e 2-4/2 =-1
mas no gabarito fala que a resposta é {4} ficarei muito grato pela ajuda.
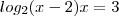
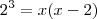
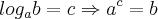
![\frac{2+\sqrt[2]{36}}{2}=\boxed{4}](/latexrender/pictures/622cb4d3b37b89504a0c7cfc2542ec4b.png "\frac{2+\sqrt[2]{36}}{2}=\boxed{4}")
, o que não seria plausível aplicar no logaritmo.
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)