Você terá que passar o -1 para o outro lado da inequação, ficando assim:
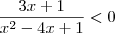
3x + 1 = 0
3x = -1
x =


Resolvendo essa equação do 2º grau acharemos as raízes:
x' =
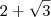
x'' =

Montando o quadro-produto, fica assim:
---------2 -raiz 3 ------------------------------------------------2 + raiz 3---------
+.......................
_.......................
_..................................
+-----------------------------------1/3 ------------------------------------------------
_.......................
_.......................
+...................................
+----------------------------------------------------------------------------------------
_.......................
+.......................
_.....................................
+-----------------------
-----------------------------------------------------------
------S = x E R / 2 -

< x < 1/3 ou 2 +

< x}
Espero que tenha entendido, valeu!




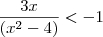


![\left[x\varepsilon\Re/-4<x<-2 ou 1<x<2 \right] \left[x\varepsilon\Re/-4<x<-2 ou 1<x<2 \right]](/latexrender/pictures/4ed5996f179a4e6b35d495d43a632077.png)

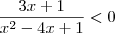


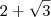

 < x < 1/3 ou 2 +
< x < 1/3 ou 2 +  < x}
< x}

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
