![g(x)=\frac{\sqrt[2]{1+3x}}{x+1} g(x)=\frac{\sqrt[2]{1+3x}}{x+1}](/latexrender/pictures/a7f8745c7240fbe0e5c166bc06ae2bef.png)
![h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[ h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[](/latexrender/pictures/9e4dade81c11385c9aeb59d03e706ccc.png)
Obrigado

![g(x)=\frac{\sqrt[2]{1+3x}}{x+1} g(x)=\frac{\sqrt[2]{1+3x}}{x+1}](/latexrender/pictures/a7f8745c7240fbe0e5c166bc06ae2bef.png)
![h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[ h(x)=\frac{x}{\left({x}^{2}-1 \right)\left(x+1 \right)},xe \right]]-1,1 \left[](/latexrender/pictures/9e4dade81c11385c9aeb59d03e706ccc.png)




 .
. . Note que nesse caso teremos que
. Note que nesse caso teremos que  e
e  . Portanto, basta resolver:
. Portanto, basta resolver: 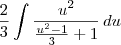 .
.

 , temos que
, temos que 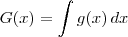 é uma primitiva de g.
é uma primitiva de g.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)