 por pmfae » Seg Mar 14, 2011 16:49
por pmfae » Seg Mar 14, 2011 16:49
Olá pessoal, sou novo aqui e estou precisando de uma ajudinha...O problema é o seguinte: "Encontrar os números a1 e a2 tais que w=a1v1+a2v2, sendo v1=(1,-2,1), v2=(2,0,4) e w=(-4,-4,14)."
Tentei resolver multiplicando a1 e a2 pelas coordenadas e montando um sistema.Cheguei a a1=2 e a2=-3. O problema é que
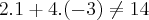
.
Se puderem me ajudar, agradeço...
Abraçoo
-
pmfae
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 14, 2011 16:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por LuizAquino » Seg Mar 14, 2011 17:02
por LuizAquino » Seg Mar 14, 2011 17:02
pmfae escreveu:"Encontrar os números a1 e a2 tais que w=a1v1+a2v2, sendo v1=(1,-2,1), v2=(2,0,4) e w=(-4,-4,14)."
Isso resulta no sistema:
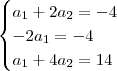
Note que esse sistema não tem solução! Isso significa que
w não pode ser escrito como combinação linear de
v1 e
v2.
Para que o sistema tivesse solução seria necessário, por exemplo, que
w=(-4,-4,-10). Desse modo, aconteceria
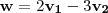
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por pmfae » Seg Mar 14, 2011 17:10
por pmfae » Seg Mar 14, 2011 17:10
Hum...foi o que eu pensei, mas é mais provável que eu estivesse errado do que o professor e o livro do qual ele copiou ahushuhasuhauhasu...
Mas então ok, muitíssimo obrigado!
-
pmfae
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 14, 2011 16:27
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VETORES]Alguém me ajuda com vetores?
por LAZAROTTI » Seg Set 17, 2012 00:49
- 2 Respostas
- 7365 Exibições
- Última mensagem por young_jedi

Seg Set 17, 2012 11:28
Geometria Analítica
-
- [Vetores] Módulo e Versor de vetores
por LAZAROTTI » Sáb Set 22, 2012 22:42
- 1 Respostas
- 2989 Exibições
- Última mensagem por young_jedi

Sáb Set 22, 2012 22:50
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5210 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
-
- [Vetores] Vetores iguais
por KleinIll » Dom Nov 04, 2012 12:17
- 2 Respostas
- 3402 Exibições
- Última mensagem por KleinIll

Dom Nov 04, 2012 13:50
Geometria Analítica
-
- [Vetores] Operações com vetores
por IlgssonBraga » Qui Jul 18, 2013 11:42
- 1 Respostas
- 2376 Exibições
- Última mensagem por Russman

Qui Jul 18, 2013 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.
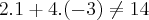 .
.
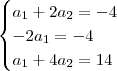
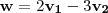 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

