-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478199 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532116 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495641 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706546 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2123012 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Paulod22 » Seg Mar 07, 2011 01:18
por Paulod22 » Seg Mar 07, 2011 01:18
Boa noite a todos.
Estou tento problemas para resolver uma questão sobre limites. Eu faço, só que resposta não bate com a do gabarito, e eu não sei onde estou errando...
Aqui está a questão:
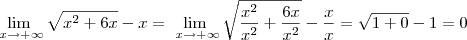
A resposta do gabarito é 3.
O método que eu utilizei foi dividir por x, mas pelo jeito não deu certo.
Obrigado desde já!
-

Paulod22
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mar 03, 2011 10:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mecatrônica
- Andamento: cursando
 por LuizAquino » Seg Mar 07, 2011 10:22
por LuizAquino » Seg Mar 07, 2011 10:22
Paulod22 escreveu:Boa noite a todos.
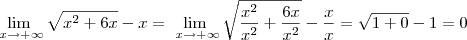
A resposta do gabarito é 3.
O método que eu utilizei foi dividir por x, mas pelo jeito não deu certo.
Se você apenas divide por x, então você alterou a expressão que você tinha antes. Você deveria dividir e multiplicar por x para que a expressão não se altere.
Por exemplo, se x não é zero, então

. Mas,
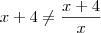
(exceto para x=1 ou x=-4).
De qualquer modo, para esse limite você deveria começar multiplicando e dividindo por
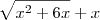
. Tente fazer e poste aqui a sua solução.
Editado pela última vez por
LuizAquino em Seg Mar 07, 2011 13:27, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Paulod22 » Seg Mar 07, 2011 12:10
por Paulod22 » Seg Mar 07, 2011 12:10
Eu tentei dividir por x porque assim facilitaria a resolução, pois a maioria dos termos iriam tender a zero.
Eu só não entendi a parte de "alterar a expressão". O que eu fiz não foi bem o que você mostrou no exemplo.
No meu caso estava assim:
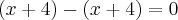
E eu fiz isso:

Se você atribuir um valor a x (4 por exemplo), você verá que continuará dando zero.
Mas tentarei pelo jeito que você falou, e postarei o resultado.
-

Paulod22
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mar 03, 2011 10:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mecatrônica
- Andamento: cursando
 por LuizAquino » Seg Mar 07, 2011 12:54
por LuizAquino » Seg Mar 07, 2011 12:54
Paulod22 escreveu:Eu só não entendi a parte de "alterar a expressão".
Para qualquer x não nulo (diferente de 1 e de -4) que você escolha, a expressão x+4 tem valor diferente da expressão

.
Por outro lado, para qualquer x não nulo que você escolha, a expressão x+4 tem valor igual a expressão
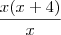
.
Paulod22 escreveu:O que eu fiz não foi bem o que você mostrou no exemplo.
No meu caso estava assim:
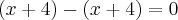
E eu fiz isso:

Errado! O cálculo de um limite é uma coisa e achar a solução de uma equação é outra coisa!
Além disso, note que:
As equações
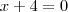
e

possuem a mesma solução: x=-4.
Já as equações

e

possuem soluções distintas!
No primeiro caso as equações foram equivalentes devido ao fato do segundo membro ser apenas o zero. Portanto, ao dividirmos toda a equação por x o segundo membro continua igual a 0.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Paulod22 » Ter Mar 08, 2011 01:28
por Paulod22 » Ter Mar 08, 2011 01:28
Fiz do jeito que você falou, multipliquei e dividi pelo conjugado.
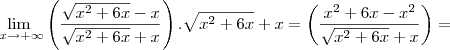
Dividindo tudo por x:
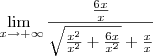
=

E deu certo. Muito obrigado pela ajuda!
Mas ainda tenho dúvida quanto à divisão. Quero entender direito para não errar mais nisso.
Pelo que eu pude perceber, se eu dividir tudo por x eu estarei alterando a equação.
Então, a resolução do limite abaixo também está errada? (Esse limite ai eu tinha resolvido anteriormente, mas como o resultado bateu eu nem desconfiei que tava errado

)

-

Paulod22
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mar 03, 2011 10:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mecatrônica
- Andamento: cursando
 por LuizAquino » Ter Mar 08, 2011 09:27
por LuizAquino » Ter Mar 08, 2011 09:27
Paulod22 escreveu:Fiz do jeito que você falou, multipliquei e dividi pelo conjugado.
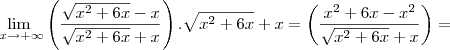
Dividindo tudo por x:
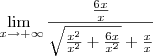
=

Apenas uma correção. No desenvolvimento de um limite você sempre deve escrever a notação "lim" em cada passo, exceto no último quando o limite é calculado. Isto é, ao invés de escrever
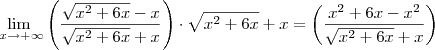
você deve escrever
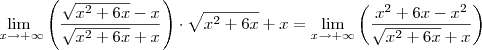
.
Paulod22 escreveu:Mas ainda tenho dúvida quanto à divisão. Quero entender direito para não errar mais nisso.
Pelo que eu pude perceber, se eu dividir tudo por x eu estarei alterando a equação.
Então, a resolução do limite abaixo também está errada? (Esse limite ai eu tinha resolvido anteriormente, mas como o resultado bateu eu nem desconfiei que tava errado

)

Sim, está errada. Foi apenas uma mera coincidência você ter obtido a reposta correta. Perceba como no exemplo anterior você usou a mesma estratégia e havia chegado na reposta errada do exercício. Além disso, novamente você não usou a notação adequada em cada passo.
Vejamos a solução correta.
Como o cosseno é uma função contínua em todo o seu domínio, podemos "retirá-la" do limite. Além disso, vamos multiplicar e dividir a expressão no limite por

.

Após aplicar o produto notável no numerador, nós dividimos tanto o numerador quanto o denominador por

. Após as simplificações, ficamos com:


É interessante destacar que nesse exercício se tivéssemos dividido o numerador e o denominador por
x ao invés de

, não poderíamos resolver o limite, pois teríamos uma indeterminação do tipo 0/0. Veja como ficaria:
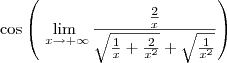
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Paulod22 » Ter Mar 08, 2011 10:55
por Paulod22 » Ter Mar 08, 2011 10:55
Ok, muito obrigado pela correção e pelas dicas!
-

Paulod22
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Mar 03, 2011 10:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Mecatrônica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites]Ajuda nessa questão sobre limite
por IlgssonBraga » Sáb Jan 25, 2014 15:53
- 1 Respostas
- 2821 Exibições
- Última mensagem por Russman

Sáb Jan 25, 2014 17:51
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2381 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- Sobre Limites
por thiagosaadoficial » Seg Fev 29, 2016 17:08
- 0 Respostas
- 1326 Exibições
- Última mensagem por thiagosaadoficial

Seg Fev 29, 2016 17:08
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 4460 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda sobre limites
 por MJC » Ter Mai 06, 2008 12:41
por MJC » Ter Mai 06, 2008 12:41
- 8 Respostas
- 17607 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 00:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 79 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
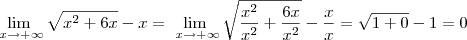


 . Mas,
. Mas, 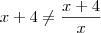 (exceto para x=1 ou x=-4).
(exceto para x=1 ou x=-4).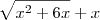 . Tente fazer e poste aqui a sua solução.
. Tente fazer e poste aqui a sua solução.
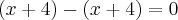

 .
.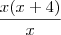 .
.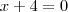 e
e  possuem a mesma solução: x=-4.
possuem a mesma solução: x=-4. e
e  possuem soluções distintas!
possuem soluções distintas!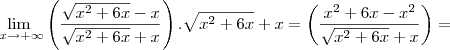
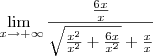 =
= 
 )
)
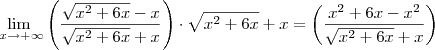 você deve escrever
você deve escrever 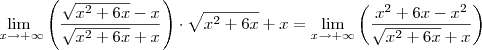 .
.
 .
.
 . Após as simplificações, ficamos com:
. Após as simplificações, ficamos com:

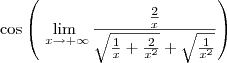


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.