boa noite, estamos com um problema e já tentamos alguns cálculos e até falei com um professor, mas não chegamos a uma resolução.
Alugamos uma casa e vamos dividir em salas comerciais. Atribuimos uma pontuação diferenciad?a para cada sala, de acordo com critérios de ventilação, iluminação, banheiros e etc, e chegamos a uma pontuação por sala que ficou da seguinte forma: SL01-8p, SL02-7p, SL03-13p, SL04-12p, SL05-10p e SL06-14p. A metragem de cada sala é: SL01-6,90m²?; SL02-12m²; SL03-9,60m²?; SL04-13,30m?²; SL05-17,50m?² e SL06-17,50m?². O valor total da área útil das salas é R$ 257,40, o valor das áreas comuns foi dividido de forma equanime. O problema é que não estamos sabendo como atribuir a pontuação a cada sala, relacionada com a metragem das mesmas, para chegar ao valor por sala. É possível fazer esse cáclculo?
semelo@gmai?l.com


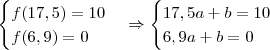
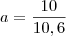 e
e  . Ou seja, a sua função é
. Ou seja, a sua função é 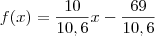 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
