 por douglasjro » Qui Jan 13, 2011 12:50
por douglasjro » Qui Jan 13, 2011 12:50
(MACK) - Sejam
a e
b as raízes da equação
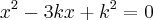
, tais que
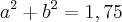
. Determinar
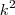
.
Resposta:0,25
Obrigado.
Douglas Oliveira
-
douglasjro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Jan 10, 2011 18:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Processos Gerenciais
- Andamento: cursando
 por VtinxD » Qui Jan 13, 2011 14:35
por VtinxD » Qui Jan 13, 2011 14:35
Tente manipular as relações de soma e produto da equação do segundo grau:
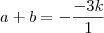
e
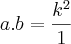
.
Se ainda não stiver conseguindo ver a solução depois eu posto a minha,mas sugiro que tente mais um pouco.
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por douglasjro » Sex Jan 14, 2011 13:25
por douglasjro » Sex Jan 14, 2011 13:25
Por favor me ajude, essa questão não consegui resolver,
Obrigado.
Douglas Oliveira
-
douglasjro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Jan 10, 2011 18:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Processos Gerenciais
- Andamento: cursando
 por VtinxD » Sex Jan 14, 2011 14:41
por VtinxD » Sex Jan 14, 2011 14:41
Será um prazer ajudar.Eleve a primeira expressão ao quadrado:

.Perceba que vc ja tem o valor do produto a.b e tambem ja tem o valor da soma

.Logo você ja tem o valor de k.
Espero ter ajudado.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por douglasjro » Sex Jan 14, 2011 18:06
por douglasjro » Sex Jan 14, 2011 18:06
Muito obrigado. 
Douglas Oliveira
-
douglasjro
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Seg Jan 10, 2011 18:59
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Processos Gerenciais
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7431 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 12742 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 11699 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- [Equação da reta] Encontrando equação paramétrica.
por Vitor Sanches » Qua Jun 26, 2013 17:54
- 0 Respostas
- 5942 Exibições
- Última mensagem por Vitor Sanches

Qua Jun 26, 2013 17:54
Geometria Analítica
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8426 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
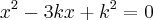 , tais que
, tais que 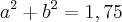 . Determinar
. Determinar 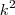 .
.
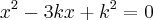 , tais que
, tais que 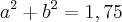 . Determinar
. Determinar 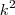 .
.
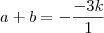 e
e 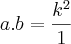 .
.

 .Perceba que vc ja tem o valor do produto a.b e tambem ja tem o valor da soma
.Perceba que vc ja tem o valor do produto a.b e tambem ja tem o valor da soma  .Logo você ja tem o valor de k.
.Logo você ja tem o valor de k.


 .
.



