Olá Rodrigo, boa noite, seja bem-vindo!
Este problema é bem interessante!
Em meu curso de graduação não cheguei a ver séries de Fourier, pois o assunto estava fora do escopo. Em Análise e Cálculo II, o mais próximo que cheguei foram as séries de Taylor e Maclaurin.
Entretanto, estudei um pouco sobre o assunto para tentar ajudá-lo.
1ª PARTE - CURIOSIDADEEm primeiro lugar, talvez você já saiba, mas quero comentar uma curiosidade histórica que li.
Ver
bibliografia:
5 - EVES, Howard. Introdução à história da matemática. Tradução: Hygino H. Domingues. Campinas, SP: Editora da UNICAMP, 2004.
Esta expressão,

também é chamada de série de Euler, pois conforme registros históricos, em carta de 1673, Oldenburg consultou Leibniz sobre a soma desta série:

Leibniz não soube responder e, em 1689, Jakob Bernoulli confessou que também não sabia a resposta.
Na época, Euler, a partir de observações sobre polinômios finitos, assumiu que suas propriedades também valiam para séries infinitas.
Partindo desta série de Taylor (ou de Maclaurin - um caso particular da série de Taylor),

o argumento de Euler iniciou-se dividindo ambos os membros por

:

Como as raízes de
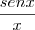
ocorrem exatamente quando

, com
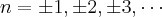
, ele escreveu a série infinita como um produto de fatores lineares dados por suas raízes, assim como fazemos com polinômios finitos, veja:


Se nós fizéssemos a distributiva deste produto, apenas pensando nos termos

, perceberíamos que o coeficiente de

em
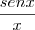
é:

Mas, na série infinita original, na expansão de
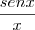
, o coeficiente de

é

. Então, estes coeficientes são iguais:
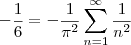
Daqui, multiplicando ambos os membros por
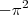
, obtemos o resultado procurado da soma:
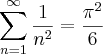
Este problema ficou conhecido como "problema da Basiléia" (Basel problem).
Basiléia é uma cidade suíça, onde nasceram Euler e a família Bernoulli.
2ª PARTE - O SEU PROBLEMARodrigo, o assunto comentado anteriormente sobre Euler pode ser facilmente encontrado na internet, além da bibliografia e outros livros.
Você viu que partindo da série de Taylor também podemos mostrar o resultado da soma.
De qualquer forma, o seu problema sugere o uso de uma série de Fourier.
Um exercício também interessante seria estudar como obter aquela expressão da série dada, eis a teoria sobre séries de Fourier: obter os coeficientes de Fourier, analisar funções pares e ímpares, integrar etc.
Adicionalmente, uma visão resumida sobre a "idéia" deste assunto é: reescrever funções periódicas através da soma infinita de senos e cossenos! Esta soma também pode ser escrita utilizando exponenciais de números complexos, considerando a famosa fórmula de Euler:

.
Enfim, voltando para o seu problema, eu quis pensar que aquele dado da séria de Fourier tinha que facilitar e não dificultar!
Um detalhe: vale colocar parênteses aqui para evitar confusão:
A série de Fourier de g(x) é:
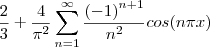
O
primeiro passo é destacar que o que queremos mostrar também pode ser escrito assim (como escrito no final da primeira parte):
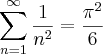
Apenas estamos reescrevendo a soma dos termos da série através do símbolo somatório.
Pois bem, o
segundo passo é "enxergar" a função periódica g(x).
Caso não visualize mentalmente, faça o gráfico no papel!
Apenas destacando o domínio
![\left[ -1, 1 \right] \left[ -1, 1 \right]](/latexrender/pictures/72fa2cc17c06fcc9e2b6f0e16acb8089.png)
, temos um trecho de uma parábola côncava para baixo, com raízes em
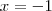
e

. Este trecho da função se repete periodicamente em toda a extensão do domínio!
Esta etapa é importante porque vemos que a função é par. E entendemos o motivo de não haver o coeficiente b de Fourier na expressão dada (pois a função seno é impar, o produto resultante também, logo a integral é nula).
Nesta etapa analisando g, constatamos que
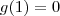
(vamos utilizar este dado depois).
Como
terceiro passo, precisamos comparar o dado que temos com o que queremos mostrar.
Olhando este somatório, percebemos uma série alternada:
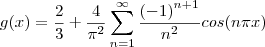
Veja em destaque, sem o fator cosseno:
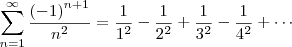
Pensando: a soma que buscamos é bem parecida, exceto pela alternância!
O fator cosseno está lá para nos ajudar, desde que usemos o dado implícito
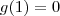
, pois quando

,
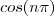
também vai alternar entre

e

.
Vamos reescrever g, quando

:

Agora, considerando o fator do cosseno alternando entre

e

, vamos observar como está o somatório:
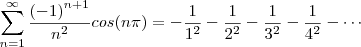
Todos os termos ficaram negativos! Então, vamos colocar

em evidência:
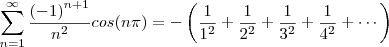
Veja o que temos: a nossa soma apareceu!

Agora, basta substituir em

:
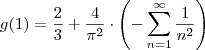
Como
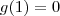
, temos:
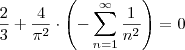
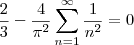
Agora basta você isolar o somatório e terá mostrado que o resultado da soma é

.
Espero ter ajudado.
Bons estudos!
 ,
, 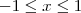 , periódica de período 2.
, periódica de período 2. 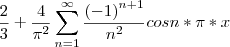


 ,
, 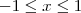 , periódica de período 2.
, periódica de período 2. 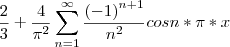





 :
:
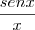 ocorrem exatamente quando
ocorrem exatamente quando  , com
, com 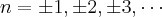 , ele escreveu a série infinita como um produto de fatores lineares dados por suas raízes, assim como fazemos com polinômios finitos, veja:
, ele escreveu a série infinita como um produto de fatores lineares dados por suas raízes, assim como fazemos com polinômios finitos, veja:

 , perceberíamos que o coeficiente de
, perceberíamos que o coeficiente de  em
em 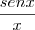 é:
é:
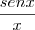 , o coeficiente de
, o coeficiente de  é
é  . Então, estes coeficientes são iguais:
. Então, estes coeficientes são iguais: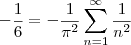
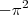 , obtemos o resultado procurado da soma:
, obtemos o resultado procurado da soma: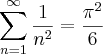
 .
.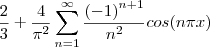
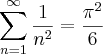
![\left[ -1, 1 \right] \left[ -1, 1 \right]](/latexrender/pictures/72fa2cc17c06fcc9e2b6f0e16acb8089.png) , temos um trecho de uma parábola côncava para baixo, com raízes em
, temos um trecho de uma parábola côncava para baixo, com raízes em 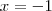 e
e  . Este trecho da função se repete periodicamente em toda a extensão do domínio!
. Este trecho da função se repete periodicamente em toda a extensão do domínio!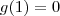 (vamos utilizar este dado depois).
(vamos utilizar este dado depois).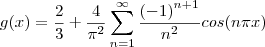
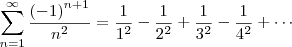
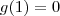 , pois quando
, pois quando  ,
, 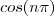 também vai alternar entre
também vai alternar entre  e
e  .
. :
:
 e
e  , vamos observar como está o somatório:
, vamos observar como está o somatório: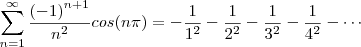
 em evidência:
em evidência: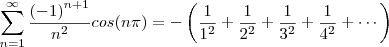

 :
: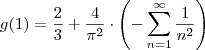
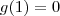 , temos:
, temos: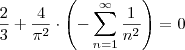
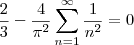
 .
.




 .
.
 :
: