por plugpc » Qui Jul 10, 2008 19:15
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
por admin » Qui Jul 10, 2008 20:32
pela diferença:
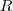da esfera é dado, o cálculo do volume da esfera é imediato:
é dada, falta o raio 
da base: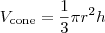
, basta você anotar os valores dados no desenho e perceberá que é um dos catetos do triângulo retângulo menor. Já temos as medidas do outro cateto e da hipotenusa, então, resta aplicar o teorema de Pitágoras.
.
por plugpc » Qui Jul 10, 2008 21:14
por admin » Sex Jul 11, 2008 03:42
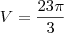01. Um cone reto com altura medindo 3 está inscrito em uma esfera com raio medindo 2, como ilustrado a seguir:
- esfera_cone.jpg (5.14 KiB) Exibido 7101 vezes
Qual o volume da região do interior da esfera que é exterior ao cone?
A)
B)
C)
D)
E)
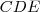, pelo teorema de Pitágoras, obtemos o raio procurado, para então finalizarmos o problema calculando o volume pedido.Voltar para Geometria Espacial
por deividchou » Ter Ago 18, 2015 15:57
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
zig escreveu:
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.
