por JustForFun » Sex Nov 05, 2010 22:42
por JustForFun » Sex Nov 05, 2010 22:42
Olá amigos! Td bem?
Estou sentindo dificuldade em resolver alguns exercícios de trigonometria e gostaria muitíssimo que me ajudassem.

Sabendo que cos(x) = 1/3 e que 3pi/2 < x <2pi, calcule:
a) sen(x + pi/6)
Eu acho que devo estar cometendo erros de matemática básica pois nunca consigo chegar à solução final!
Sei que ao mostrar 3pi/2 < x < 2pi (a mesma coisa que 270°< x < 360°) o exercício me diz que x encontra-se no 4 quadrante. Depois, tenho que utilizar a fórmula sen(a+b)= sen a.cos b + sen b.cos a para
chegar à solução. Acredito que durante a resolução do exercício também terei que me vale da fórmula sen x² + cos x² = 1, já que foi me dado apenas o valor do cos(x) e não do sen(x).
Ficaria muito grato se alguém puder me dar uma explicação detalhada de como resolver o problema.
Agradeço desde já!
Obs.: Infelizmente senti dificuldade para escrever o problema em LaTeX. Espero que compreendam.
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por andrefahl » Sáb Nov 06, 2010 01:41
por andrefahl » Sáb Nov 06, 2010 01:41
AHSUdHASUDHA
eu ia responde mas foram mais rapido!!
=)
e ia ser igualzinho =D
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por JustForFun » Sáb Nov 06, 2010 04:52
por JustForFun » Sáb Nov 06, 2010 04:52
Primeiramente obrigado aos dois amigos pelo interesse em ajudar!

Agora vamos lá, a parte chata. Primeiro gostaria que conferissem se eu fiz certo essa parte:
sen² + cos² = 1
sen² + (1/3)² = 1
sen² + 1/9 = 1
sen² = 1 - 1/9
sen² = 8/9
sen = + ou - raiz de 8/9 (no caso, o sinal considerado será o negativo, já que seno no 4 quadrante é menor que 0)
Caso eu tenha feito certo gostaria de aprender como que esse "menos raiz de 8/9" se transforma em -2 raiz de dois/3 como foi mostrado pelo colega acima.
Desde já agradeço!
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por andrefahl » Sáb Nov 06, 2010 10:02
por andrefahl » Sáb Nov 06, 2010 10:02
Bom é o seguinte é soh tirar a raiz e fatorar o numero de cima =)
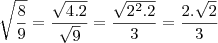
só simplificações =)
mas se deixasse o
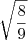
em resp dissertativa estaria certo tb a unica coisa eh que
em uma alternativa vc teria dificuldade para achar a resp.
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por JustForFun » Sáb Nov 06, 2010 19:34
por JustForFun » Sáb Nov 06, 2010 19:34
Muitíssimo obrigado andrefahl!
Agora a dúvida final

-2 raiz de 2/3 x raiz de 3/2 = - 1/3 raiz de 6?
Você cortou o dois de cima com o de baixo? Então como apareceu esse 1?
Vlw!
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Nov 06, 2010 22:26
por Molina » Sáb Nov 06, 2010 22:26
JustForFun escreveu:Muitíssimo obrigado andrefahl!
Agora a dúvida final

-2 raiz de 2/3 x raiz de 3/2 = - 1/3 raiz de 6?
Você cortou o dois de cima com o de baixo? Então como apareceu esse 1?
Vlw!
Boa noite.
Procure utilizar o
Editor de Fórmulas nas expressões matemáticas, pois se eu colocar 2+3/8 não dá para saber se estou somando dois com três oitavos ou somando dois com três e dividindo por oito, ok?
Quanto a sua dúvida é referente a
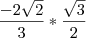
:
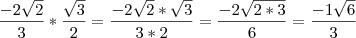

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por JustForFun » Dom Nov 07, 2010 01:22
por JustForFun » Dom Nov 07, 2010 01:22
Muito obrigado pelo resposta molina!
Agora consegui entender o exercício todo! Vlw mesmo!

Abração!
-
JustForFun
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sex Nov 05, 2010 22:16
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ajuda]trigonometria
por victorrocha31 » Dom Nov 22, 2009 20:57
- 2 Respostas
- 3383 Exibições
- Última mensagem por victorrocha31

Seg Nov 23, 2009 00:34
Trigonometria
-
- ajuda em trigonometria
 por buzinaaroo » Qua Nov 10, 2010 10:05
por buzinaaroo » Qua Nov 10, 2010 10:05
- 3 Respostas
- 2398 Exibições
- Última mensagem por Jefferson

Qui Nov 18, 2010 15:44
Trigonometria
-
- [Ajuda] Trigonometria
por wallsoares » Qua Mar 23, 2011 01:25
- 4 Respostas
- 2246 Exibições
- Última mensagem por wallsoares

Qui Mar 24, 2011 01:26
Trigonometria
-
- Ajuda com trigonometria 9º ano
por AndreiOEstudioso » Sáb Abr 23, 2011 13:24
- 2 Respostas
- 2458 Exibições
- Última mensagem por AndreiOEstudioso

Dom Abr 24, 2011 11:21
Trigonometria
-
- ajuda trigonometria 11º ano
por tiagofe » Ter Abr 26, 2011 19:59
- 5 Respostas
- 3525 Exibições
- Última mensagem por tiagofe

Qua Abr 27, 2011 12:52
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



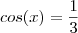 e
e 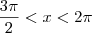 , então
, então 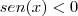





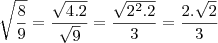
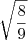 em resp dissertativa estaria certo tb a unica coisa eh que
em resp dissertativa estaria certo tb a unica coisa eh que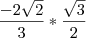 :
: