Uma empresa foi contratada para efectuar a mudança de casa da família Silva. O tempo, em minutos,
que a camioneta demora a efectuar o trajecto entre as duas casas é uma variável aleatória com
distribuição Normal. Sabe-se que a probabilidade de a camioneta demorar mais do que 20 minutos a
efectuar o trajecto entre as duas casas é de 0.0668 e a de demorar entre 10 minutos e 20 minutos é de
0.7005.
a) Qual é a probabilidade de o trajecto entre as duas casas demorar entre 10 e 15 minutos?
b) Tendo a camioneta que efectuar 9 trajectos entre as duas casas, qual é a probabilidade de demorar
menos de 2 horas a efectuá-los todos?
c) Suponha que a camioneta tem que fazer 9 trajectos entre as duas casas:
c1) Quantos trajectos se podem esperar que demorem mais do que 15 minutos a fazer?
c2) Qual é a probabilidade de todos os trajectos terem sido efectuados, cada um, no máximo, em 15
minutos?
nao consigo resolver este problema, ja tentei descobrir a media atraves de ir ver as standerizações, mas nao consigo chegar ao valor da media nem do desvio padrao e sem estes nao consigo resolver este problema.tnh um mini-teste amanha e vai sair um exercico mt semelhante...


 .
. é a sua variável, tal que
é a sua variável, tal que  , então:
, então:
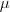 e
e  .
. .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)