![\left( \sqrt{\sqrt[3]{5}\sqrt{5}\right) ^8 e 2^{-3/4}](/latexrender/pictures/e65ea191073ec4332b95ad15964858d5.png "\left( \sqrt{\sqrt[3]{5}\sqrt{5}\right) ^8 e 2^{-3/4}")
é?
por Elcioschin » Qui Out 07, 2010 14:53
por Rogerio Murcila » Qui Out 07, 2010 15:09
por MarceloFantini » Qui Out 07, 2010 15:31
![\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8](/latexrender/pictures/951a1144974cd18112f3523db8dd79ef.png "\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8")
e 
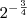são?![\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8 = \left( \sqrt{ \sqrt[6]{5^5} } \right)^8 = \left( \sqrt[12]{5^5} \right)^8 = 5^{\frac{10}{3}} = 5^3 \cdot \sqrt[3]{5}](/latexrender/pictures/ec124a009e943f66d6be9606b0361925.png "\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8 = \left( \sqrt{ \sqrt[6]{5^5} } \right)^8 = \left( \sqrt[12]{5^5} \right)^8 = 5^{\frac{10}{3}} = 5^3 \cdot \sqrt[3]{5}")
![2^{-\frac{3}{4}} = \frac{1}{2^{\frac{3}{4}}} = \frac{1}{\sqrt[4]{2^3}} = \frac{1}{\sqrt[4]{8}}](/latexrender/pictures/bd48f8b0d8bb5b0b3b8f51b0838b8df7.png "2^{-\frac{3}{4}} = \frac{1}{2^{\frac{3}{4}}} = \frac{1}{\sqrt[4]{2^3}} = \frac{1}{\sqrt[4]{8}}")
por natanskt » Qui Out 07, 2010 16:33
![25\frac{\sqrt[4]{2}}{2}](/latexrender/pictures/ea4dca891139ac064236d39616b69e65.png "25\frac{\sqrt[4]{2}}{2}")
![5\frac{\sqrt[4]{2}}{2}](/latexrender/pictures/f8ec1a1a79a896051857c5c606eab405.png "5\frac{\sqrt[4]{2}}{2}")
![5{\sqrt[4]{8}}](/latexrender/pictures/196636a76461c09063ea432d4174ccd3.png "5{\sqrt[4]{8}}")
![25{\sqrt[4]{8}}](/latexrender/pictures/c3ce7f803493c0fb080c4e75876c6ac8.png "25{\sqrt[4]{8}}")
por Rogerio Murcila » Qui Out 07, 2010 16:37
![\left( \sqrt { \sqrt[3]{5} \cdot \sqrt[3]{5} } \right)^8*{2e^{-\frac{3}{4}}](/latexrender/pictures/669cca80bda2b103ee3fed7390e7df24.png "\left( \sqrt { \sqrt[3]{5} \cdot \sqrt[3]{5} } \right)^8*{2e^{-\frac{3}{4}}")
![\sqrt[3]{5}](/latexrender/pictures/4a3076b52907a89cc91dc134ecd1fc75.png "\sqrt[3]{5}")
só no primeiro termo, outra coisa considerei o "e" como logaritmo natural na base e, afinal ele pergunto: "a resposta é?" Tudo no singular. ![\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8*{e*2^{-\frac{3}{4}}](/latexrender/pictures/2847edb104694a1063822670dee0c6db.png "\left( \sqrt { \sqrt[3]{5} \cdot \sqrt{5} } \right)^8*{e*2^{-\frac{3}{4}}")
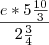= 345,4793 em decimalpor Rogerio Murcila » Qui Out 07, 2010 17:11
![\left( \sqrt { \sqrt[3]{5\sqrt{5}}} \right)^8*{2^{-\frac{3}{4}}](/latexrender/pictures/841b5fbdd168ed07f6e0a861fed8c6c2.png "\left( \sqrt { \sqrt[3]{5\sqrt{5}}} \right)^8*{2^{-\frac{3}{4}}")
= 14,865 em decimalpor Rogerio Murcila » Qui Out 07, 2010 17:25
![{2}^{-3/4}=\frac{1}{2}\sqrt[4]{2}](/latexrender/pictures/64da97050eb11908df4763743c9fd7b0.png "{2}^{-3/4}=\frac{1}{2}\sqrt[4]{2}")
![{\sqrt[3]{5\sqrt[2]{5}}}^{4} = 25](/latexrender/pictures/56eb19ff3c2ec433fd2b6113ddba62e1.png "{\sqrt[3]{5\sqrt[2]{5}}}^{4} = 25")
= 14,865 em decimal
por AlexKidd » Dom Ago 12, 2012 12:40
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)