Após o enunciado, vcs poderão ver os raciocínios que usei até agora
e espero bastante que vcs contribuam...
-> Um grupo de amigos decidiu preparar cestas contendo 4 itens distintos cada, a serem enviadas para os desabrigados de Alagoas. Esses 4 itens devem ser escolhidos entre 8 tipos de produtos de limpeza, 5 tipos de alimentos não perecíveis e 7 tipos de agasalho. Em cada cesta, deve haver pelo menos um item que seja alimento não perecivel, pelo menos um item que seja produto de limpeza e pelo menos um item que seja agasalho. Quantos tipos de cestas distintas podem ser feitas?
R:
Foi feita a proposta de solucionar esta questão através de combinação.
Assim, para facilitar o raciocínio, vamos supor que só farão parte das cestas os produtos de higiene e os alimentos.
Temos:
I)
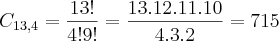
Considerando produtos de limpeza e alimentos sem restrições
Em seguida:
II)
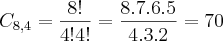
Considerando as cestas que possam ser feitas apenas com os produtos de higiene.
Prosseguindo:
III)

Considerando as cestas que possam ser feitas apenas com os alimentos.
Assim, ao subtrair as cestas apenas com alimentos e as cestas apenas com os produtos de higiene das cestas que têm tudo, teremos cestas que possuem pelo menos um elemento de cada,ou seja, pelo menos um alimento e pelo menos um produto de higiene:
I - II - III:
715 - 70 - 5 = 640
Mas, e ao incluirmos nas cestas os agasalhos?
Seguindo o mesmo raciocício, calcuremos as cestas compostas por todos os tipos sem restrições, depois subtrairemos as cestas apenas com alimentos, as cestas apenas com produtos de higiene e as cestas apenas com agasalhos. Mas isso não oferece o resultado pedido, pois apenas exclui as cestas compostas por exclusividades (apenas com um tipo). É perfeitamente possível haver dentre essas cestas uma que contenha um agasalho e três alimentos, por exemplo.
E é aqui que surge minha dúvida. Como fazer para garantir, através de combinações, que haja em cada cesta, pelo menos um tipo de produto proposto.
Aguardo respostas.
Abraço
Daniel carvalho




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.