 por Joana Gabriela » Seg Ago 09, 2010 11:00
por Joana Gabriela » Seg Ago 09, 2010 11:00
Um fazendeiro dividiu 30 km2 de suas terras entre seus 4 filhos, de idades distintas, de modo que as áreas
dos terrenos recebidos pelos filhos estavam em progressão geométrica, de acordo com a idade, tendo
recebido mais quem era mais velho. Ao filho mais novo coube um terreno com 2 km2 de área.
O filho que tem idade imediatamente superior à do mais novo recebeu um terreno de área igual a:
A) 10 km2
B) 8 km2
C) 4 km2
D) 6 km2
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por Molina » Seg Ago 09, 2010 15:17
por Molina » Seg Ago 09, 2010 15:17
Joana Gabriela escreveu:Um fazendeiro dividiu 30 km2 de suas terras entre seus 4 filhos, de idades distintas, de modo que as áreas
dos terrenos recebidos pelos filhos estavam em progressão geométrica, de acordo com a idade, tendo
recebido mais quem era mais velho. Ao filho mais novo coube um terreno com 2 km2 de área.
O filho que tem idade imediatamente superior à do mais novo recebeu um terreno de área igual a:
A) 10 km2
B) 8 km2
C) 4 km2
D) 6 km2
Boa tarde, Joana.
A primeira forma que me veio a mente é usar a fórmula da soma de PG:

onde,

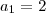

Substituindo esses valores e resolvendo, você chegaria numa equação incompleta do 4° grau para achar o
q (razão). Não é difícil encontrar qual será esse valor. Feito isso basta multiplicar a razão pelo primeiro termo e você chega no resultado do problema.
Bom estudo.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Joana Gabriela » Ter Ago 10, 2010 16:07
por Joana Gabriela » Ter Ago 10, 2010 16:07
Eu não sei resolver essa equação !
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por MarceloFantini » Qua Ago 11, 2010 05:44
por MarceloFantini » Qua Ago 11, 2010 05:44
Tente fatorar ou encontrar uma raíz e aplicar Briot-Ruffini.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Joana Gabriela » Qua Ago 11, 2010 11:22
por Joana Gabriela » Qua Ago 11, 2010 11:22
A equação ficou assim:
30 = 2 (1 - {q}^{4})
1 - q
qx30 = 2 - 2 {q}^{4}
-2{q}^{4} + 30q + 2 = 0 *(-1)
2{q}^{4} - 30q - 2 = 0
Dai eu não sei mais resolver
Agradeço desde já a ajuda !
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
 por Molina » Qua Ago 11, 2010 21:43
por Molina » Qua Ago 11, 2010 21:43
Chuta

que vai dar certo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Joana Gabriela » Sex Ago 13, 2010 10:38
por Joana Gabriela » Sex Ago 13, 2010 10:38
Deu naum !
-
Joana Gabriela
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Jul 28, 2010 10:13
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Agroecologia
- Andamento: cursando
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ESTATISTICA UFRN 2001
por Joana Gabriela » Qui Ago 05, 2010 11:47
- 1 Respostas
- 5332 Exibições
- Última mensagem por MarceloFantini

Qui Ago 05, 2010 16:39
Matemática Financeira
-
- LOGARITMO - Questão 40 - Vestibular 2012 UFRN
por Anastacia Vaz » Dom Abr 07, 2013 12:03
- 2 Respostas
- 7211 Exibições
- Última mensagem por nakagumahissao

Dom Abr 14, 2013 14:34
Logaritmos
-
- Matrizes B^2001
por Vagner Almeida » Ter Fev 24, 2009 20:36
- 4 Respostas
- 3057 Exibições
- Última mensagem por Vagner Almeida

Dom Mar 01, 2009 15:59
Matrizes e Determinantes
-
- Uerj 2001 - questão sobre conjuntos
por sspmat61 » Qui Mar 10, 2011 15:16
- 4 Respostas
- 14816 Exibições
- Última mensagem por Abelardo

Sex Mar 11, 2011 22:43
Álgebra Elementar
-
- Geometria Espacial - Cones - UFMG 2001
por felip3mg » Ter Dez 06, 2011 12:16
- 1 Respostas
- 2421 Exibições
- Última mensagem por joao_pimentel

Qua Dez 14, 2011 21:06
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




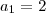



 que vai dar certo.
que vai dar certo.

 .
.



