Dificuldade na expressã numérica

[mazoni]

2) 52 pessoas discutem a preferência por dois produtos A e B, entre outros e conclui-se que o número de pessoas que gostavam de B era:
I - O quadruplo do número de pessoas que gostavam de A e B;
II - O dobro do número de pessoas que gostavam de A;
III - A metade do número de pessoas que não gostavam de A nem de B.
Nessas condições, o número de pessoas que não gostavam dos dois produtos é igual a:
a) 48
b) 35
c) 36
d) 47
e) 37

Pessoal, estou perdindo nesse exercício, eu sou péssico em matemática, porém preciso muito aprender.





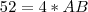
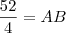
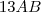aqui mostra que 13 pessoas gostam de A e B?

Pessoal eu tenho muita dificuldade de entender os enunciados dos exercícios, por favor me ajudem.

[gustavowelp]

Boa tarde Mazoni.

Acho que estás se esquecendo do "ENTRE OUTROS".

52 pessoas não discutem SOMENTE A e B. Discutem C, D...

Eu também estava tentando resolver, mas me incluo naqueles que não souberam resolver...

Se alguém souber, gostaria(mos) de saber a solução.

Um abraço a todos!