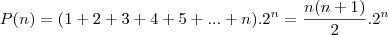por henrique25 » Sáb Mai 08, 2010 17:07
por henrique25 » Sáb Mai 08, 2010 17:07
Nao sei se este lugar é adequado entao desculpem.Tenho um problema de recorrencia que nao consigo achar a "forma geral" , é necessario apenas isso p/ resolver o resto eu sei.
O Problema:
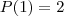
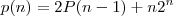
Eu fiz assim mas ta errado:
n=2 -
![2.[2P(n-2)+[n2^n-1] + n2^n 2.[2P(n-2)+[n2^n-1] + n2^n](/latexrender/pictures/460f60cbf390651c764a86d2a5f1f2ad.png)
n=3 -
![2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n 2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n](/latexrender/pictures/88f78c8fc5d0ff722055213810d8be1e.png)
n=4 -
![2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n 2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n](/latexrender/pictures/d3b1c87240d214b9db4082c4efa71627.png)
forma geral:
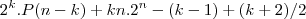
Ai fiz:
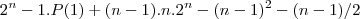
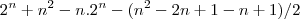
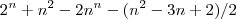
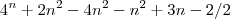
Ai deu isso aqui,mas quando substituo nao da certo.
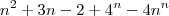
Tem uma formula tbm mas nao consegui:
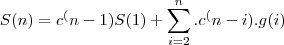
Gostaria que vcs deem dicas de como fazer la em cima so o" n2^n" , porque se fosse um numero eu saberia mas"elevado à n" ta complicado.Se vcs puderem ajudar estarei mt grato.Obrigado
-
henrique25
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Mai 08, 2010 15:13
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: informatica
- Andamento: cursando
 por Douglasm » Sáb Mai 08, 2010 18:49
por Douglasm » Sáb Mai 08, 2010 18:49
Olá henrique, de início eu não entendi muito bem a questão, mas creio que você queria achar uma fórmula geral para
P(n) sem precisar recorrer ao termo anterior. Sendo assim, eu simplesmente fui desenvolvendo
P(1),
P(2),
P(3), etc. e encontrei a relação geral. Veja só:
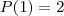
Seguindo a fórmula da recorrência:
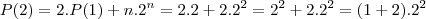
![P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3 P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3](/latexrender/pictures/4265f6482701e1ceddae66daa6875096.png)
![P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4 P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4](/latexrender/pictures/36a786b152bba4b9e85d8d509fd66762.png)
![P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5 P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5](/latexrender/pictures/afc34215ee3990bb1c6d1d836eb75a67.png)
E assim podemos continuar indefinidamente. Não sei se haveria necessidade de uma prova mais formal, uma prova por indução ou algo do tipo, mas é evidente que a fórmula geral de
P(n) é:
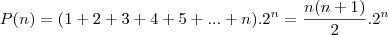
Espero ter ajudado. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- relação de recorrência - funções de Bessel
por MacGyver » Dom Nov 08, 2009 14:55
- 0 Respostas
- 2016 Exibições
- Última mensagem por MacGyver

Dom Nov 08, 2009 14:55
Cálculo: Limites, Derivadas e Integrais
-
- Relação de Recorrência - Método de substituição
por cesarxyz » Qui Abr 26, 2012 16:07
- 0 Respostas
- 1796 Exibições
- Última mensagem por cesarxyz

Qui Abr 26, 2012 16:07
Álgebra Elementar
-
- Relação de Recorrência - Máquina de vender selos
por cesarxyz » Qui Abr 26, 2012 16:02
- 0 Respostas
- 1702 Exibições
- Última mensagem por cesarxyz

Qui Abr 26, 2012 16:02
Álgebra Elementar
-
- 4y''+y'=0 qual relação recorrência? EDO em série de potência
por Felipe » Qua Mar 25, 2020 22:07
- 3 Respostas
- 3293 Exibições
- Última mensagem por adauto martins

Dom Abr 05, 2020 11:14
Equações
-
- Problema de Recorrência
por henrique25 » Dom Mai 09, 2010 16:18
- 1 Respostas
- 1579 Exibições
- Última mensagem por Elcioschin

Dom Mai 09, 2010 20:48
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
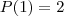
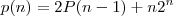
![2.[2P(n-2)+[n2^n-1] + n2^n 2.[2P(n-2)+[n2^n-1] + n2^n](/latexrender/pictures/460f60cbf390651c764a86d2a5f1f2ad.png)
![2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n 2.2.[2P(n-3)+[n2^n-2] + [n2^n -1] +n2^n](/latexrender/pictures/88f78c8fc5d0ff722055213810d8be1e.png)
![2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n 2.2.2.[2P(n-4)+[n2^n-3] [n2^n -2] +n2^n-1+n2^n](/latexrender/pictures/d3b1c87240d214b9db4082c4efa71627.png)
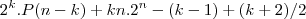
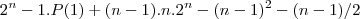
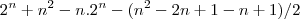
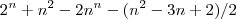
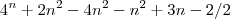
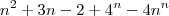
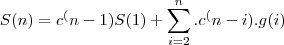


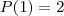
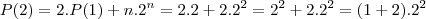
![P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3 P(3) = 2.P(2) + 3.2^3 = 2 .[(1+2).2^2] + 3.2^3 = (1+2+3).2^3](/latexrender/pictures/4265f6482701e1ceddae66daa6875096.png)
![P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4 P(4) = 2.P(3) + 4.2^4 = 2.[(1+2+3).2^3] + 4.2^4 = (1+2+3+4).2^4](/latexrender/pictures/36a786b152bba4b9e85d8d509fd66762.png)
![P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5 P(5) = 2.P(4) + 5.2^5 = 2.[(1+2+3+4).2^4] + 5.2^5 = (1+2+3+4+5).2^5](/latexrender/pictures/afc34215ee3990bb1c6d1d836eb75a67.png)