 no semi-plano
no semi-plano  . Dentre todos os retângulos com um dos lados sobre o eixo
. Dentre todos os retângulos com um dos lados sobre o eixo  e dois dos vértices em C, seja R aquele de maior perímetro. A área de R é portanto, numericamente igual a:
e dois dos vértices em C, seja R aquele de maior perímetro. A área de R é portanto, numericamente igual a:A) 4
B) 30
C) 1
D) 34


O perímetro de
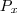 é
é
Para
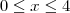 . O valor máximo de
. O valor máximo de 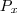 é o máximo da função
é o máximo da função 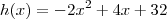 .
.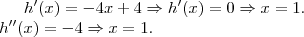 é o ponto de máximo.
é o ponto de máximo.Assim, o perímetro máximo será atingido em
Para
 , temos
, temos 
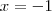 , temos
, temos  .
.Então, este retângulo tem medida 2 na base e altura igual a 15. Portanto sua área é igual a 30. (LETRA B)



 .
.
 :
: