-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478245 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532542 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496055 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 707882 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2125320 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por jmario » Qua Abr 28, 2010 13:41
por jmario » Qua Abr 28, 2010 13:41
Como se calcula o seguinte limite
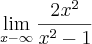
No meu gabarito a resposta é 2, mas eu não consigo chegar nesse número.
Grato
Mario
Editado pela última vez por
jmario em Qua Abr 28, 2010 14:16, em um total de 1 vez.
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Neperiano » Qua Abr 28, 2010 13:56
por Neperiano » Qua Abr 28, 2010 13:56
Ola
Você poderia usar a definição da derivada para resolver, mas creio ser mais facil pelas tecnicas de diferenciação
((4x)(x^2-1)-(2x^2)(2x))/(x^2-1)^2
4x^3-4x-4x^2/x^4-1
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por jmario » Qua Abr 28, 2010 14:14
por jmario » Qua Abr 28, 2010 14:14
E para calcular o limite?
No meu gabarito a resposta é 2 e eu não consigo chegar nesse número.
Grato
Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qua Abr 28, 2010 15:40
por Douglasm » Qua Abr 28, 2010 15:40
Olá Mario. Creio que seja evidente que a expressão tende a 2, apesar de nunca assumir de fato este valor. Veja: quando x tende ao infinito, x²-1 tende a x² e portanto o limite é 2. Talvez fique mais claro, como disse o Maligno, se usarmos as derivadas para avaliar (a Regra de L'Hopital):
Derivando o numerador e denominador, separadamente, o limite se torna:
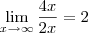
Eu omiti o processo, mas caso reste alguma duvida é só perguntar. Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 09:10
por jmario » Qui Abr 29, 2010 09:10
O problema é que eu só posso aplicar a regra de L´Hopital quando dá uma indeterminação do tipo
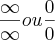
O que não é o caso desse limite porque fica o (-1) e não dá a indeterminação.
Essa é aminha dúvida caro amigo
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 09:53
por Douglasm » Qui Abr 29, 2010 09:53
Exatamente Mario. Mas pense bem: infinito é um número tão enorme que o (-1) é pequeno demais comparado a ele, é irrelevante. Por isso mesmo você tem uma indeterminação e a regra é válida.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 11:38
por jmario » Qui Abr 29, 2010 11:38
Eu consultei um professor que me passou a seguinte a resolução
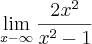
que eu não sei como ele tensformou e ficou
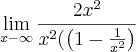
QUE TAMBÉM DEU 2
vOCÊ SABA ME DIZER como ele fez essa transformação?
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 12:15
por Douglasm » Qui Abr 29, 2010 12:15
Realmente, assim é mais simples de entender. O que foi feito foi o seguinte:
Seu professor pegou o denominador,

, e colocou

em evidência. Veja só:
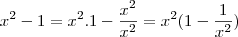
Temos então:
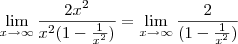
Agora é só perceber que quando x tende ao infinito, o denominador
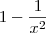
tende a ser 1. (note que
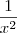
é um número infinitamente pequeno nesse caso, portanto tende a zero.)
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 13:14
por jmario » Qui Abr 29, 2010 13:14

Eu não consegui entender essa colocação do

em evidência
Por que ficou
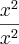
e depois ele vira

Por que o

vira 1 e o denominador continua

se o

está multiplicando também.
Se o

do numerador vira 1 porque o

do denomimador também não vira 1
Não entendi, vc pode me explicar essa passagem?
Grato
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 13:29
por Douglasm » Qui Abr 29, 2010 13:29
Olá Mario. Isso é simples, veja só:
Concorda que
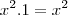
e que
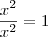
?
Vamos então fazer a substituição:
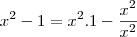
Agora é só observarmos que x^2 multiplica os dois termos então temos que:
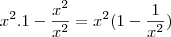
Ou seja,

multiplicado por

menos

multiplicado por

é igual ao nosso denominador
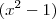
.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 13:44
por jmario » Qui Abr 29, 2010 13:44
Agora eu entendi Douglas.
Vc é muito inteligente.
Obrigado pela ajuda.
Já que vc é bem inteligente, veja se vc consegue me ajudar nessa aqui
Dada a função
g(x)= x, se x > 1

, se x
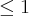
A pergunta é a seguinte a função g é diferenciável em x = 1?
Grato
Mario
Editado pela última vez por
jmario em Qui Abr 29, 2010 13:50, em um total de 2 vezes.
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 13:49
por Douglasm » Qui Abr 29, 2010 13:49
O melhor é abrir outro tópico para uma nova questão. Na verdade essa questão você mesmo postou e ela foi muito bem respondida aqui:
viewtopic.php?f=107&t=1952Editado pela última vez por
Douglasm em Qui Abr 29, 2010 13:52, em um total de 1 vez.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 13:52
por jmario » Qui Abr 29, 2010 13:52
Douglasm escreveu:O melhor é abrir outro tópico para uma nova questão, mas me diga, o que você que saber a respeito dessa função?
Dá uma olhadinha que agora eu acertei
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por jmario » Qui Abr 29, 2010 13:53
por jmario » Qui Abr 29, 2010 13:53
Dada uma função
g(x) = x, se x >1
x^3, se

A função g é diferenciável em x= 1?
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 13:54
por Douglasm » Qui Abr 29, 2010 13:54
Sim. Mas de qualquer modo, ela foi respondida pelo Elcioschin no outro tópico que você abriu, veja lá. =)
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por jmario » Qui Abr 29, 2010 13:56
por jmario » Qui Abr 29, 2010 13:56
Vc não pode explicar do seu jeito, porque eu não entendi muito bem a explicação dele.
Grato
Mario
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
 por Douglasm » Qui Abr 29, 2010 14:11
por Douglasm » Qui Abr 29, 2010 14:11
Para falar a verdade, eu não sei um jeito melhor de explicar isso que o dele. (Que aliás está bem elucidativo.) Se você pensar que para um função ser derivável, ela deve apresentar derivadas laterais idênticas quando x tende a um determinado valor, no seu caso o 1, verá que essa sua função que forma um "bico" não é derivável nesse ponto. Me desculpe, mas realmente não sei explicar de um jeito mais simples.
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qui Abr 29, 2010 17:43
por MarceloFantini » Qui Abr 29, 2010 17:43
Crie um novo tópico em todo caso para tentarmos ajudá-lo, o motivo principal é pra não acumular dúvidas diferentes em um mesmo lugar, porque depois fica difícil de fazer referência.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por victorbahia » Dom Mai 02, 2010 16:12
por victorbahia » Dom Mai 02, 2010 16:12
Caro Mário!
Tem uma forma muito mais simples de se achar este limite.
Existe um macete que toda vez que o limite tende a infinito (ou menos infinito), basta você pegar o termo de maior grau do numerador e o termo de maior grau do denominador. Pronto...
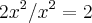
-
victorbahia
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Mai 02, 2010 15:49
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Dom Mai 02, 2010 18:13
por Neperiano » Dom Mai 02, 2010 18:13
Ola
Eu postei errado confundi lim com derivada
Nesta questão, basta você pegar os termos de mais valor emcima e embaixo e dividir
2x^2/x^2=1
Se por acaso der x na resposta é sinal que o limite vai para infinito ou 0, dependendo donde estiver o x.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por jmario » Sex Mai 07, 2010 13:56
por jmario » Sex Mai 07, 2010 13:56
Douglasm escreveu:Para falar a verdade, eu não sei um jeito melhor de explicar isso que o dele. (Que aliás está bem elucidativo.) Se você pensar que para um função ser derivável, ela deve apresentar derivadas laterais idênticas quando x tende a um determinado valor, no seu caso o 1, verá que essa sua função que forma um "bico" não é derivável nesse ponto. Me desculpe, mas realmente não sei explicar de um jeito mais simples.
Até a próxima.
Eu coloquei um novo desafio de derivada Douglas, veja se vc pode me ajudar?
-
jmario
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Qui Abr 15, 2010 12:23
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cáculo de limite
 por catabluma123 » Qua Fev 10, 2016 21:06
por catabluma123 » Qua Fev 10, 2016 21:06
- 9 Respostas
- 6269 Exibições
- Última mensagem por adauto martins

Qua Fev 17, 2016 11:27
Cálculo: Limites, Derivadas e Integrais
-
- Exercícios - Cáculo III
 por HenriqueGS » Dom Jun 05, 2016 20:37
por HenriqueGS » Dom Jun 05, 2016 20:37
- 1 Respostas
- 1017 Exibições
- Última mensagem por adauto martins

Ter Jun 07, 2016 12:18
Cálculo: Limites, Derivadas e Integrais
-
- Cáculo - Limites - função contínua num intervalo
por Antonio H V Araujo » Sáb Nov 14, 2015 22:24
- 1 Respostas
- 2274 Exibições
- Última mensagem por Cleyson007

Seg Nov 16, 2015 07:29
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 9793 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10218 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 103 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
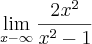

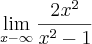



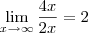

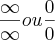


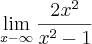
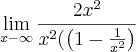

 , e colocou
, e colocou  em evidência. Veja só:
em evidência. Veja só: 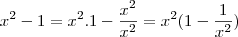
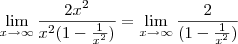
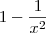 tende a ser 1. (note que
tende a ser 1. (note que  é um número infinitamente pequeno nesse caso, portanto tende a zero.)
é um número infinitamente pequeno nesse caso, portanto tende a zero.)
 Eu não consegui entender essa colocação do
Eu não consegui entender essa colocação do  em evidência
em evidência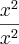 e depois ele vira
e depois ele vira 
 vira 1 e o denominador continua
vira 1 e o denominador continua  se o
se o  está multiplicando também.
está multiplicando também. do numerador vira 1 porque o
do numerador vira 1 porque o  do denomimador também não vira 1
do denomimador também não vira 1
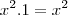 e que
e que 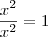 ?
?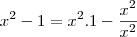
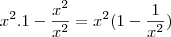
 multiplicado por
multiplicado por  menos
menos  multiplicado por
multiplicado por  é igual ao nosso denominador
é igual ao nosso denominador 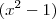 .
.
 , se x
, se x 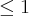










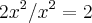





 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.



 , certo? O autor começou do primeiro membro:
, certo? O autor começou do primeiro membro:


 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
