Boa tarde. Na questão abaixo, possui três itens (a, b e c). Fiz as letras a e b, mas não consegui resolver a c. Para resolver a c, é necessário as informações da resolução dos itens anteriores, por isso, vou anexar a minha resolução e queria, por gentileza, que vocês analisassem se estão corretas e me ajudar na resolução da letra c. Segue enunciado:
No triângulo ABC, o ângulo BÂC mede 60 graus e o ângulo ABC mede 50 graus. Considere M o ponto médio do lado AB, D no prolongamento do lado BC tal que AC = CD e P o ponto sobre o lado BC tal que m(BP) = m(AC) + m(CP).
a) Com os dados do enunciado faça uma figura
b) Calcule as medidas dos ângulos internos do triângulo ACD
c) Calcule a medida do ângulo MPC (ângulo ~P)
. 
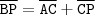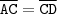. Com efeito, isto implica que:
é ponto médio do segmento 
.
. Assim, 
.
.
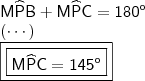por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)