Olá
Estou com duas duvidas sobre limites no infinito.
A primeira é sobre o estudo do sinal do numero proximo de zero no denominador. Ex: lim(2x5-3x²+2)/-x²+7 quando x->+infinito
A outra é sobre como identificar uma indeterminaçao do tipo "infinito-infinito", por exemplo, no seguinte limite: lim(3x5-4x³+1) quando x->+infinito
Tenho prova segunda, me ajudem rsrs
Agradeço desde já


 ;
; 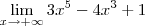 .
. cresce muito mais que
cresce muito mais que  , então o limite é infinito mesmo. Indeterminação é quando se tem
, então o limite é infinito mesmo. Indeterminação é quando se tem  . No primeiro, eu faria assim:
. No primeiro, eu faria assim: 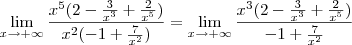 . Quando x está tendendo ao infinito,
. Quando x está tendendo ao infinito,  todos tendem a 0, sobrando
todos tendem a 0, sobrando 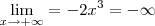 .
.

 , ai o denominador ficaria
, ai o denominador ficaria  , como
, como 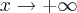 , o denominador seria 0, daí ele (o livro) fala que se for
, o denominador seria 0, daí ele (o livro) fala que se for  , no caso algum número que se aproxime de zero pela esquerda, o limite seria
, no caso algum número que se aproxime de zero pela esquerda, o limite seria  . É ai que queria saber como saber o sinal desse número aproximado de zero.
. É ai que queria saber como saber o sinal desse número aproximado de zero.