 por Flavio Cacequi » Ter Abr 03, 2018 08:47
por Flavio Cacequi » Ter Abr 03, 2018 08:47
Dada a equação biquadrada x^4-(a+13)x^2+4a=0, determine um valor de a para que a soma das raízes positivas seja 5.
)36
b)-4
c)2
d)9
e)6
-
Flavio Cacequi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jun 06, 2017 17:48
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Gebe » Ter Abr 03, 2018 14:13
por Gebe » Ter Abr 03, 2018 14:13
Não tem alternativa correta, é só conferir por um programa qualquer que, quando substituido os valores de "a" dados como alternativas e somamos as raizes positivas não chegamos ao valor 5. Como pode ser visto ao final da minha resolução temos uma possibilidade de a=36, porem este valor quando substituido nao resulta duas raizes positivas que somadas dão 5.
Claro posso ter errado algo, nesse caso me desculpe.
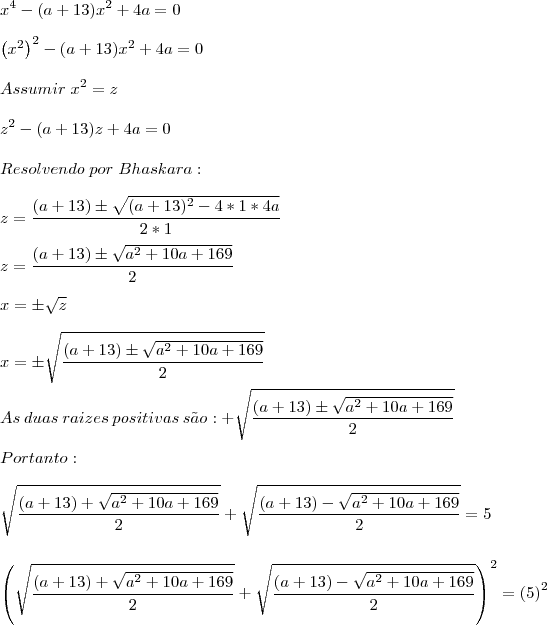
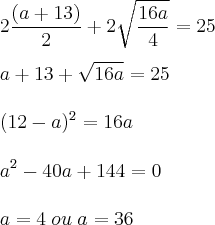
a=4 resulta em duas raizes positivas que somadas dão 5, sendo elas 4 e 1.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação polinomial] Ajuda com essa equação?
por Mkdj21 » Sáb Jan 26, 2013 16:19
- 1 Respostas
- 13011 Exibições
- Última mensagem por young_jedi

Dom Jan 27, 2013 17:15
Equações
-
- Equação Polinomial
por Cleyson007 » Dom Jun 14, 2009 16:21
- 1 Respostas
- 5993 Exibições
- Última mensagem por Cleyson007

Qua Jun 17, 2009 09:20
Polinômios
-
- Equação Polinomial
por gustavowelp » Dom Jun 27, 2010 11:53
- 3 Respostas
- 3280 Exibições
- Última mensagem por Douglasm

Dom Jun 27, 2010 12:37
Sistemas de Equações
-
- Equação polinomial
por cristina » Sáb Set 18, 2010 17:29
- 5 Respostas
- 4164 Exibições
- Última mensagem por alexandre32100

Sex Set 24, 2010 01:45
Polinômios
-
- (ITA) Equação polinomial
por Carolziiinhaaah » Sex Fev 04, 2011 15:35
- 7 Respostas
- 5914 Exibições
- Última mensagem por Renato_RJ

Qua Fev 16, 2011 00:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



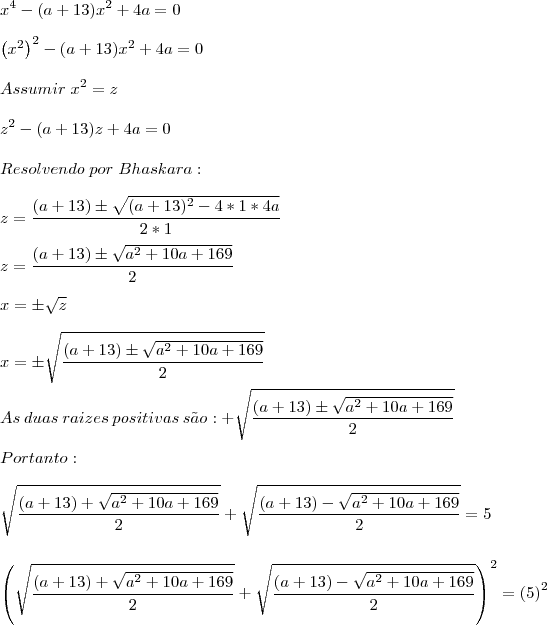
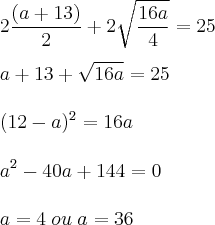


 .
.



