 por gust15 » Sex Dez 16, 2016 18:35
por gust15 » Sex Dez 16, 2016 18:35
Uma escada de 10m de comprimento está apoiada em uma parede vertical. Se a base da escada desliza afastando-se da parede a uma taxa de 0,5m/s, determine:
a) quão rápido o topo da escada está escorregando para baixo quando a base da escada está a 6m da parede?
b) O tempo necessário para que o centro de gravidade da escada desça 3m?
Bom, estava tentando resolver esse exercício. Na letra a) eu cheguei na seguinte resposta: dy/dt = -0,375 m/s
Mas na letra b) eu não sei como proceder... Se alguém puder confirmar se a resposta que encontrei na letra a) está correta e ainda me dizer como posso resolver a letra b) eu agradeceria muito
-
gust15
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Dez 16, 2016 17:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia elétrica
- Andamento: cursando
 por adauto martins » Sáb Dez 17, 2016 15:48
por adauto martins » Sáb Dez 17, 2016 15:48
a)
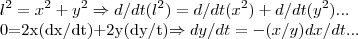
![{l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8... {l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8...](/latexrender/pictures/fdd0e774a1a6675a47869647be6ff70d.png)
,logo:
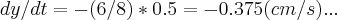
b)
o centro de massa se desloca,tanto na direçao de x,como de y...entao sua velocidade é:
![{v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s... {v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s...](/latexrender/pictures/c2f40b86794c80339d6be6771066695d.png)
na direçao y,o centro de massa sofre a açao da gravidade,portanto:
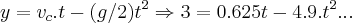
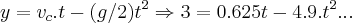
,agora é resolver essa eq.de segundo grau,p/
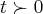
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Taxas de Variação]
por raimundoocjr » Sáb Jun 15, 2013 14:50
- 1 Respostas
- 832 Exibições
- Última mensagem por young_jedi

Sáb Jun 15, 2013 23:22
Cálculo: Limites, Derivadas e Integrais
-
- Taxas de Variação Relacionadas
por KSaito » Seg Nov 29, 2010 12:07
- 0 Respostas
- 1819 Exibições
- Última mensagem por KSaito

Seg Nov 29, 2010 12:07
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]- Taxas de variação
por Ana_Rodrigues » Qui Fev 23, 2012 21:06
- 1 Respostas
- 1292 Exibições
- Última mensagem por LuizAquino

Qui Fev 23, 2012 21:33
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas-taxas de variação
por lucas_carvalho » Ter Dez 02, 2014 20:27
- 2 Respostas
- 3321 Exibições
- Última mensagem por lucas_carvalho

Qua Dez 03, 2014 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Taxas Relacionadas] Cálculo I
por francisco0856 » Dom Mar 02, 2014 20:56
- 1 Respostas
- 1003 Exibições
- Última mensagem por Cleyson007

Seg Mar 03, 2014 09:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


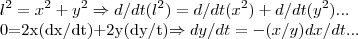
![{l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8... {l}^{2}={x}^{2}+{y}^{2}\Rightarrow y=\sqrt[]{({10}^{2}-{6}^{2}}=\sqrt[]{64}=8...](/latexrender/pictures/fdd0e774a1a6675a47869647be6ff70d.png) ,logo:
,logo: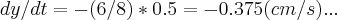
![{v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s... {v}_{c}=\sqrt[]{{dx/dt}^{2}+{dy/dt}^{2}}=\sqrt[]{{0.5}^{2}+{(-0.375}^{2}}=0.625 cm/s...](/latexrender/pictures/c2f40b86794c80339d6be6771066695d.png)
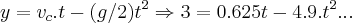
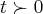 ...
...
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
