 por Ederson_ederson » Ter Jun 23, 2015 19:20
por Ederson_ederson » Ter Jun 23, 2015 19:20
Olá, estou tentando resolver uma questão dificílima:
É a questão 8 do link
http://www.futuromilitar.com.br/portal/ ... Epcar_.pdfa primeira proposição eu consegui fazer e é verdadeira
A segunda possui expoente 'n' e eu tentei começar somando e subtraindo os expoentes, mas acho que está errado porque tem um sinal de menos no meio e então eu não sei como fazer:

Eu pensei em:
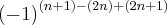
Se estiver errado, por onde eu devo começar?
Já a terceira eu consegui fazer e deu
![\frac{3(\sqrt[2]{6}+1)}{5} \frac{3(\sqrt[2]{6}+1)}{5}](/latexrender/pictures/14db4af2869de2eb4477a3b335835522.png)
portanto é falsa, certo???
Eu quebrei a cabeça, mas na segunda não consegui visualizar nada que pode ser feito...
obrigado
-
Ederson_ederson
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Jun 23, 2015 19:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Jun 27, 2015 15:14
por DanielFerreira » Sáb Jun 27, 2015 15:14
Ederson, do enunciado tiramos que
n pertence ao conjunto dos naturais não nulo. Ora,
n poderá ser par ou ímpar, e devemos analisar ambas possibilidades.
Inicialmente, resolva a expressão como se

fosse PAR; então:

é positivo;
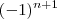
é negativo;

é negativo;
...
Lembre-se que números negativos elevados a expoentes pares resultam em números positivos; e quando elevados a expoentes ímpares são negativos!
Encontrei
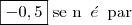
.
Conclua o exercício considerando
n ímpar. Se encontrar - 0,5; então a resposta será este valor. Entretanto, se obter outro valor saberá que é FALSA!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Ederson_ederson » Sáb Jun 27, 2015 19:49
por Ederson_ederson » Sáb Jun 27, 2015 19:49
Olá danjr5
etendi, valeu. Eu não sabia por onde começar porque estava pensando em fatoração. Com a sua explicação consegui fazer para n sendo ímpar e deu +0,5 , logo essa proposição é falsa.
Valeu!!!
-
Ederson_ederson
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Jun 23, 2015 19:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Sáb Jun 27, 2015 20:51
por DanielFerreira » Sáb Jun 27, 2015 20:51
Não há de quê! A propósito, responda quando souber, ok?!
Até a próxima, se houver!

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Ederson_ederson » Dom Jun 28, 2015 23:41
por Ederson_ederson » Dom Jun 28, 2015 23:41
Valeu... pode deixar... ajudo sempre que puder...

-
Ederson_ederson
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Ter Jun 23, 2015 19:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3534 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3575 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8204 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2483 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 1894 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

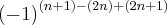
![\frac{3(\sqrt[2]{6}+1)}{5} \frac{3(\sqrt[2]{6}+1)}{5}](/latexrender/pictures/14db4af2869de2eb4477a3b335835522.png) portanto é falsa, certo???
portanto é falsa, certo???

 fosse PAR; então:
fosse PAR; então: é positivo;
é positivo;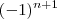 é negativo;
é negativo; é negativo;
é negativo;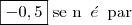 .
.
