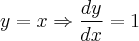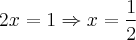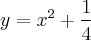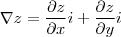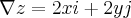1. A parábola y=x²+C deve ser tangente à reta y=x. Calcule C.
Sabendo-se que a derivada da equação da parábola nos dará a inclinação da reta passando em qualquer ponto da parábola e sabendo-se também que esta inclinação deverá ser o mesmo que o da reta dada num determinado ponto, tem-se que:

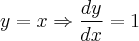
Logo,
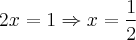
A reta tocará na parábola quando x for 1/2 e y for 1/2, ou seja, no ponto (1/2, 1/2). Usando estes valores na equação da parábola teremos:


Assim a equação da parábola ficará:
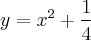
2. Mostre que a reta normal, em qualquer ponto do círculo x²+y²=a² passa pela origem.
Usando o cálculo 2, mais precisamente o conceito de Gradiente, tem-se que:

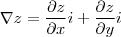
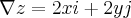
Que por sua vez são as próprias retas x e y que sempre passam por (0,0) como queríamos demonstrar.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali