Olá Estela, seja bem-vinda!
Sobre o que você pensou, considere o seguinte:
A equação da circunferência nos diz que o raio é 2.
E se a aresta do hexágono regular medisse 4, ele não caberia inscrito na circunferência de raio 2.
Estes passos ajudarão você a entender a solução:
Encontre o ângulo central do polígono regular, neste caso, um hexágono.
Sendo

este ângulo, em radianos você pode encontrá-lo assim:

Ou, em graus:

Ou seja, como o raio da circunferência é 2, o primeiro argumento é que podemos dividir o hexágono em seis triângulos isósceles.
Mas, como

e a soma dos ângulos internos de todo triângulo é
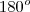
, segue que os demais ângulos internos também são
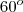
, logo, cada triângulo é equilátero.
Após você desenhar ou pensar na figura, perceberá que então basta encontrar as distâncias
h e
c, pois assim terá as coordenadas do ponto
V que é um vértice.

- hexagono_regular.jpg (24.96 KiB) Exibido 7477 vezes
Você deverá encontrar que
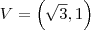
.
Para calcular h, considere que é a altura do triângulo equilátero de lado 2.
E c, você pode obter por Pitágoras, ou simplesmente por simetria, pois a medida c é metade do lado do triângulo.
Enfim, após obter
V acima, por simetria (reflexão nos eixos) você obtém os demais vértices do hexágono.
São todos eles, no sentido anti-horário:
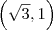

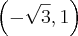



Espero ter ajudado!


 este ângulo, em radianos você pode encontrá-lo assim:
este ângulo, em radianos você pode encontrá-lo assim:

 e a soma dos ângulos internos de todo triângulo é
e a soma dos ângulos internos de todo triângulo é 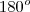 , segue que os demais ângulos internos também são
, segue que os demais ângulos internos também são 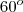 , logo, cada triângulo é equilátero.
, logo, cada triângulo é equilátero.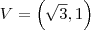 .
.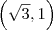

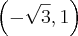





 .
.
 :
: