 por Subnik » Sex Abr 03, 2015 19:43
por Subnik » Sex Abr 03, 2015 19:43
Calcule o limite:
![\lim_{x\rightarrow+/-\infty}\sqrt[]{x^2-x.\Pi}-\sqrt[]{x^2-1} \lim_{x\rightarrow+/-\infty}\sqrt[]{x^2-x.\Pi}-\sqrt[]{x^2-1}](/latexrender/pictures/8c7f1500438fe60757fb897c9e5fe62f.png)
Resposta:

-
Subnik
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 03, 2015 19:31
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Sáb Abr 04, 2015 12:14
por adauto martins » Sáb Abr 04, 2015 12:14
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por DanielFerreira » Sáb Abr 04, 2015 12:23
por DanielFerreira » Sáb Abr 04, 2015 12:23
Olá
Subnik,
seja bem-vindo!
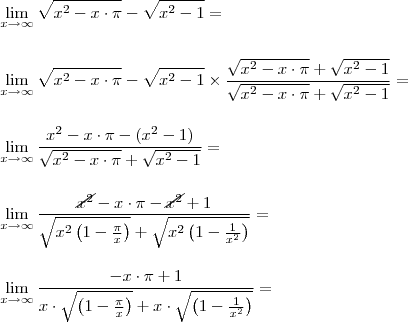

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5408 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4753 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4779 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4807 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2792 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow+/-\infty}\sqrt[]{x^2-x.\Pi}-\sqrt[]{x^2-1} \lim_{x\rightarrow+/-\infty}\sqrt[]{x^2-x.\Pi}-\sqrt[]{x^2-1}](/latexrender/pictures/8c7f1500438fe60757fb897c9e5fe62f.png)


![L=\lim_{x\rightarrow \infty}{x}^{2}(\sqrt[]{1-\pi/x}-\sqrt[]{1-1/{x}^{2}}) L=\lim_{x\rightarrow \infty}{x}^{2}(\sqrt[]{1-\pi/x}-\sqrt[]{1-1/{x}^{2}})](/latexrender/pictures/6731087004ef601ee06aa0819ec44cad.png) =
=![\lim_{x\rightarrow \infty}{x}^{2}(\sqrt[]{1-\pi/x}-\sqrt[]{1-1/{x}^{2}}).(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}}/(\sqrt[]{1+\pi/x}+\sqrt[]{1-1/{x}^{2}}) \lim_{x\rightarrow \infty}{x}^{2}(\sqrt[]{1-\pi/x}-\sqrt[]{1-1/{x}^{2}}).(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}}/(\sqrt[]{1+\pi/x}+\sqrt[]{1-1/{x}^{2}})](/latexrender/pictures/6cc1cb3adfadb2ae957e11b9c15a652e.png) =
=![\lim_{x\rightarrow \infty}{x}^{2}(1-\pi/x-1-1/{x}^{2})/\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})=\lim_{x\rightarrow \infty}-(\pi.x+1)/(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})= \lim_{x\rightarrow \infty}{x}^{2}(1-\pi/x-1-1/{x}^{2})/\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})=\lim_{x\rightarrow \infty}-(\pi.x+1)/(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})=](/latexrender/pictures/e943b2e95b004ffee6cdb038673aa188.png) =
=![\lim_{x\rightarrow \infty}-( \pi x + 1)/\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}}) \lim_{x\rightarrow \infty}-( \pi x + 1)/\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})](/latexrender/pictures/0a37057a51e6e4e6ea9a1c9c14da8f0a.png) =
=![\lim_{x\rightarrow \infty}-x(\pi+1/x)/(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}}) \lim_{x\rightarrow \infty}-x(\pi+1/x)/(\sqrt[]{1-\pi/x}+\sqrt[]{1-1/{x}^{2}})](/latexrender/pictures/69322c445ece8eaac302e7094ab5cafc.png) =
=![\lim_{x\rightarrow \infty}-(\pi+1/{x}^{2})/(\sqrt[]{1/{x}^{2}-\pi/{x}^{3}}+\sqrt[]{1-1/{x}^{4}}=-\pi/2 \lim_{x\rightarrow \infty}-(\pi+1/{x}^{2})/(\sqrt[]{1/{x}^{2}-\pi/{x}^{3}}+\sqrt[]{1-1/{x}^{4}}=-\pi/2](/latexrender/pictures/9c94fb37b733d5112afdb7f220e3fb78.png)

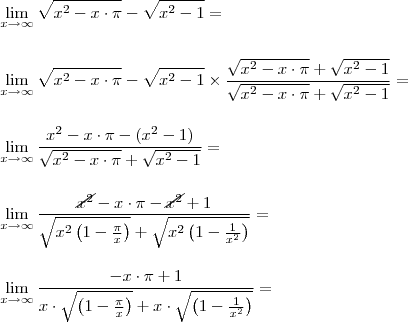




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.