Eu tenho dois valores... X e Y...
X1 = Y1
E
X2= Y2... Ou seja, tenho dois limites...
Neste caso eu tenho
600 = 0.1
900 = 1
O meu objectivo é descobrir o valor de Y (sendo ele proporcional ao do X) entre cada um dos limites.... Por Exemplo:
se 600 = 0.1
E
900 = 1
Quanto equivale o Y ao numero 780? Ou Talvez o numero 820? O meu objectivo é enquanto o X sobe/Desce... o Y sobe/desce proporcionalmente ao X tendo em conta os dois limites...
Eu já tentei as seguintes formas sem sucesso...
600 + 900 / (o valor que eu disse Ex:) 700;
tambem tentei
600 + 900 / (o valor que eu quero Ex:) 700 + 600;
E tentei outra forma que não me lembro, mas também não deu resultado...
Por exemplo, eu sei que a metade de ambos seria:
750 = 0.55;
Mas não consigo achar forma de resolver este problema... Agradecia imenso uma ajuda
 !
!

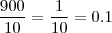
 e os correspondentes
e os correspondentes  .
.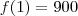 e
e 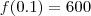 .
.

 .
.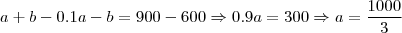 e
e 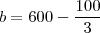 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
