Seja a equação
 , em que A, B e C são números reais. Pode-se afirmar que:
, em que A, B e C são números reais. Pode-se afirmar que:( ) A= 2, B= 3 e C= 1
( ) A= 1, B= 4 e C= 2
( ) A= 3, B= 2 e C= -1
( ) A= 5, B= 3 e C= 0
( ) A = B = C

 , em que A, B e C são números reais. Pode-se afirmar que:
, em que A, B e C são números reais. Pode-se afirmar que:
![\frac{x}{a} + \frac{y}{b} = ]\frac{bx+ay}{ab} \frac{x}{a} + \frac{y}{b} = ]\frac{bx+ay}{ab}](/latexrender/pictures/1e6a265501ec89105e4daf3269e69500.png) .
. buscar duas outras tais que somadas resultem nesta. Em geral, isto é feito quando c não é primo.
buscar duas outras tais que somadas resultem nesta. Em geral, isto é feito quando c não é primo.  . Note que 15=3.5. Assim, buscamos duas constantes A e B tais que
. Note que 15=3.5. Assim, buscamos duas constantes A e B tais que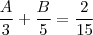 .
.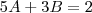 .
. e o polinômio
e o polinômio  tem n raízes reais ,então é possível mostrar que existem n números
tem n raízes reais ,então é possível mostrar que existem n números  tais que
tais que 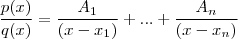
 denota a i-ésima raízes real simples de
denota a i-ésima raízes real simples de  .
. e
e 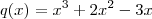 . Note que
. Note que  tem três raízes reais simples respectivamente,
tem três raízes reais simples respectivamente, 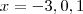 . Assim, devem existir tres números reais, por exemplo, A,B e C tais que
. Assim, devem existir tres números reais, por exemplo, A,B e C tais que 
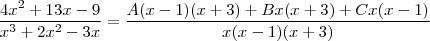
 . Assim, agrupando os termos no denominador da freação da direita e simplificando
. Assim, agrupando os termos no denominador da freação da direita e simplificando  obtemos
obtemos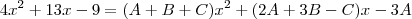

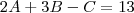

 ,
,  e
e  .
.


Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.