[Limites]: Limite Trigonométrico (cotangente)

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Limites]: Limite Trigonométrico (cotangente)

Regras do fórum
Responder

[Limites]: Limite Trigonométrico (cotangente)

Mensagempor magalhaesari » Seg Set 08, 2014 15:33

Olá pessoal! Estou tentando essa questão há tempos e ainda não consegui chegar ao gabarito informado no wolfphramalfa. Minha dúvida surge com esse segundo termo (Vx-Va), não sei se devo analisálo como uma parte da cotangente ou um termo separadamente em multiplicação. Das últimas vezes, multipliquei duas vezes pelo termo conjugado e o resultado final foi: 1/4Va, quando o gabarito informado é: 1/4a.Va

Como estudo sozinha (minhas aulas ainda não começaram) não sei como fazer por l'hôspital, como já vi em uma resolução.
Anexos
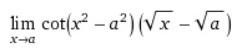
Sem título.jpg
Sem título.jpg (4.23 KiB) Exibido 1150 vezes
magalhaesari
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Seg Set 08, 2014 15:25
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Civil
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo a=\sqrt{8}+ i em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja \alpha o ângulo entre o eixo horizontal e o afixo a. O triângulo é retângulo com catetos 1 e \sqrt{8}, tal que tg \alpha = \frac{1}{sqrt{8}}. Seja \theta o ângulo complementar. Então tg \theta = \sqrt{8}. Como \alpha + \theta = \frac{\pi}{2}, o ângulo que o afixo b formará com a horizontal será \theta, mas negativo pois tem de ser no quarto quadrante. Se b = x+yi, então \frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}. Como módulo é um: |b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}.

Logo, o afixo é b = \frac{1 + i\sqrt{8}}{3}.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum