Encontremos a equação da reta
r:
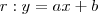
- sabe-se que a inclinação da reta corresponde ao coeficiente angular; e, o mesmo é dado cálculo da tangente de tal ângulo;
- o ponto (- 1, 0) pertence à reta.
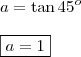
Daí,

Segue que,
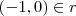
. Com isso,

Por fim,
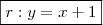
De maneira análoga encontramos a equação da reta
s, dada por
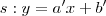
- sabe-se que a inclinação da reta corresponde ao coeficiente angular; e, o mesmo é dado cálculo da tangente de tal ângulo;
- o ponto (2, 0) pertence à reta.
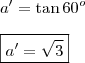
Daí,
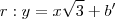
Segue que,

. Com isso,

Por fim,

Para encontrar a intersecção, especificamente em Ox, igualamos os Y's, veja:
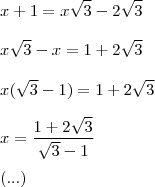
Espero ter ajudado!



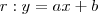
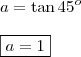

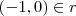 . Com isso,
. Com isso,
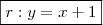
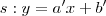
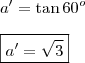
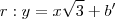
 . Com isso,
. Com isso,

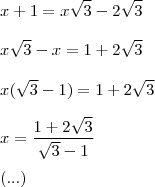


 .
.



