por cortesfsa » Sex Dez 18, 2009 22:30
por cortesfsa » Sex Dez 18, 2009 22:30
Dúvida: usando a definição de limites, se formos demonstrar que

, podemos proceder da seguinte forma:
Devemos mostrar que

Nota-se que
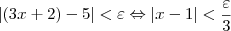
Assim, se escolhermos
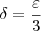
, teremos

De fato, se

Agora, como faço para demonstrar, usando a definição, que

é falso?
Bronze OBQ Norte/Nordeste
---
"Try not. Do, or do not. There is no try." --Yoda
"Computer, compute to the last digit the value of pi" --Spock
"I have a bad feeling about this..." --Obi-Wan
-
cortesfsa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 18, 2009 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Molina » Sáb Dez 19, 2009 15:15
por Molina » Sáb Dez 19, 2009 15:15
Boa tarde.
Note que suponde que o resultado desse limite seja 6 você não conseguirá chegar que
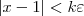
. Com isso não conseguirá escolher um

e dar continuidade a demonstração.
Acredito que esse critério já é suficiente para mostrar que o limite não é 6.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por cortesfsa » Sáb Dez 19, 2009 19:22
por cortesfsa » Sáb Dez 19, 2009 19:22
Olá molina,
Ainda não me dei por satisfeito

E se eu proseguir da seguinte forma:
![\[\LARGE\\ |(3x+2)-6|<\varepsilon \\ |3x-4|<\varepsilon \\ -\varepsilon <3x-4<\varepsilon \\ \frac{4-\varepsilon }{3}<x<\frac{4+\varepsilon }{3} \\ \frac{1-\varepsilon }{3}<x-1<\frac{1+\varepsilon }{3}\] \[\LARGE\\ |(3x+2)-6|<\varepsilon \\ |3x-4|<\varepsilon \\ -\varepsilon <3x-4<\varepsilon \\ \frac{4-\varepsilon }{3}<x<\frac{4+\varepsilon }{3} \\ \frac{1-\varepsilon }{3}<x-1<\frac{1+\varepsilon }{3}\]](/latexrender/pictures/b37bf8fcbea090811ad142891c4a2a82.png)
Isso significa que se

estiver dentro desse intervalo a condição estará satisfeita? Eu sei que, pelo
conceito de limite isso é absurdo, mas eu só estou tentando entender a
definição.
Outra dúvida: como chegar em

demonstrando
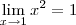
?
Agradeço a atenção

Bronze OBQ Norte/Nordeste
---
"Try not. Do, or do not. There is no try." --Yoda
"Computer, compute to the last digit the value of pi" --Spock
"I have a bad feeling about this..." --Obi-Wan
-
cortesfsa
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Dez 18, 2009 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Molina » Sáb Dez 19, 2009 19:54
por Molina » Sáb Dez 19, 2009 19:54
cortesfsa escreveu:Outra dúvida: como chegar em

demonstrando
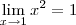
?
Vamos lá:
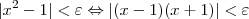
Mas,


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- [Limites]Preciso de ajuda para calcular alguns limites
por Pessoa Estranha » Ter Jul 16, 2013 17:15
- 2 Respostas
- 4750 Exibições
- Última mensagem por LuizAquino

Qua Jul 17, 2013 09:12
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4774 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4803 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2787 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , podemos proceder da seguinte forma:
, podemos proceder da seguinte forma:
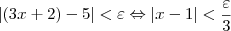
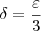 , teremos
, teremos

 é falso?
é falso?
 , podemos proceder da seguinte forma:
, podemos proceder da seguinte forma:
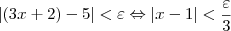
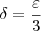 , teremos
, teremos

 é falso?
é falso?
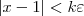 . Com isso não conseguirá escolher um
. Com isso não conseguirá escolher um  e dar continuidade a demonstração.
e dar continuidade a demonstração.


![\[\LARGE\\ |(3x+2)-6|<\varepsilon \\ |3x-4|<\varepsilon \\ -\varepsilon <3x-4<\varepsilon \\ \frac{4-\varepsilon }{3}<x<\frac{4+\varepsilon }{3} \\ \frac{1-\varepsilon }{3}<x-1<\frac{1+\varepsilon }{3}\] \[\LARGE\\ |(3x+2)-6|<\varepsilon \\ |3x-4|<\varepsilon \\ -\varepsilon <3x-4<\varepsilon \\ \frac{4-\varepsilon }{3}<x<\frac{4+\varepsilon }{3} \\ \frac{1-\varepsilon }{3}<x-1<\frac{1+\varepsilon }{3}\]](/latexrender/pictures/b37bf8fcbea090811ad142891c4a2a82.png)
 estiver dentro desse intervalo a condição estará satisfeita? Eu sei que, pelo conceito de limite isso é absurdo, mas eu só estou tentando entender a definição.
estiver dentro desse intervalo a condição estará satisfeita? Eu sei que, pelo conceito de limite isso é absurdo, mas eu só estou tentando entender a definição. demonstrando
demonstrando 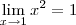 ?
?

demonstrando
?