Ok , vamos tentar ,não vou formalizar (tenta fazer isso), respondo sem objetividade e com mais detalhes . Só mudando as notações e seguindo a mesma linha de raciocínio .
Faz-se hipótese que

, isto é ,
i)
Para todo 
dado ,
existe um [t]

(dependente de

) tal que se

pertence a

) então

[f avaliado em x] está no intervalo

.
OBS.1. Para estabelecer uma relação entre
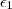
e
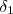
as notações entre parêntesis são mais convenientes .
OBS.2. Excluímos o ponto

do intervalo para enfatizar que a função não necessariamente está definida em

( possa ser que

) . Mas, uma condição é necessária ,

obrigatoriamente deve está definida em
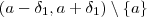
,em outras palavras
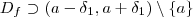
.
OBS.3. Se alguma propriedade
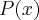
é verdadeira sempre que
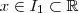
.Se

então
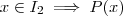
. No momento certo vamos fazer menção a está observação .
ii) Da mesma forma definimos o segundo limite .
Agora queremos mostrar que
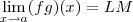
. Como em todas demostrações , rascunhamos de trás para frente . Escreva

( o mesmo para g , usando L ) e utilize desigualdade triangular para obtermos

(pois

e
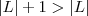
.
(Observe que

para todo M, enquanto nem sempre
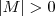
(possa ser que
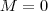
, assim em geral não podemos definir

a menos que considerarmos 1° M = 0 e depois diferente de zero . Veremos isto a seguir )
Se dado qualquer

encontramos um
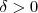
correspondente tal que cada parcela seja menor ou igual a
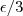
,então por transitividade [Se
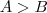
e
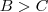
então
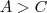
] o resultado segue . E é isto que vamos fazer .
Para todo

dado , temos que

. Assim dá hipótese dos limites existirem , segue de (i) e (ii) que existe
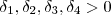
para os quais
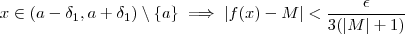

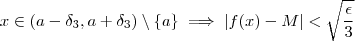

Agora defina
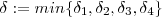
. Note que

e
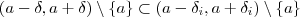
para cada
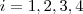
(Pq?) .
(Por isso adotei esta notação , para notares que todas vizinhanças de

acima contém

) [Usando a notação mais comum também é fácil ver ,
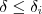
e se

, por transitividade ,
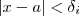
](i=1,2,3,4).
Dá observação

seque-se que
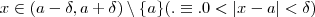
então todas implicações acima são verdadeiras . Daí ,

.
Impressionante a qualidade do artigo , muito bem escrito . Porém há um erro de digitação lá que é muito comum (por isso estou aq editando meu erros de digitação ) , acredito que a intenção era escrever
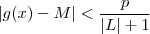
ao invés de
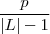
(pq isto automaticamente implica que

e podemos ter

e
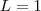
) . Observe que troquei

por

, mas acho que não atrapalhará no entendimento .
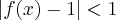 , não sei de onde o 1 veio;
, não sei de onde o 1 veio;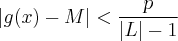



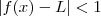 . Vê se lá que faz-se hipótese que o limite
. Vê se lá que faz-se hipótese que o limite 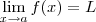 existe o que significa que para cada
existe o que significa que para cada  dado , existe
dado , existe  tal que
tal que 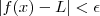 sempre que
sempre que 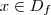 satisfaz
satisfaz 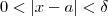 . Em particular se tomarmos
. Em particular se tomarmos  existe
existe  tq
tq  .
. 
 , isto é ,
, isto é ,  dado ,
dado ,  (dependente de
(dependente de  pertence a
pertence a ) então
) então  [f avaliado em x] está no intervalo
[f avaliado em x] está no intervalo  .
. 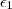 e
e 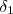 as notações entre parêntesis são mais convenientes .
as notações entre parêntesis são mais convenientes .  do intervalo para enfatizar que a função não necessariamente está definida em
do intervalo para enfatizar que a função não necessariamente está definida em  ) . Mas, uma condição é necessária ,
) . Mas, uma condição é necessária ,  obrigatoriamente deve está definida em
obrigatoriamente deve está definida em 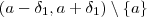 ,em outras palavras
,em outras palavras 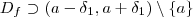 .
.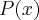 é verdadeira sempre que
é verdadeira sempre que 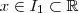 .Se
.Se  então
então 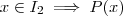 . No momento certo vamos fazer menção a está observação .
. No momento certo vamos fazer menção a está observação . 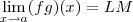 . Como em todas demostrações , rascunhamos de trás para frente . Escreva
. Como em todas demostrações , rascunhamos de trás para frente . Escreva  ( o mesmo para g , usando L ) e utilize desigualdade triangular para obtermos
( o mesmo para g , usando L ) e utilize desigualdade triangular para obtermos 
 e
e 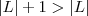 .
. para todo M, enquanto nem sempre
para todo M, enquanto nem sempre 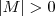 (possa ser que
(possa ser que 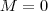 , assim em geral não podemos definir
, assim em geral não podemos definir  a menos que considerarmos 1° M = 0 e depois diferente de zero . Veremos isto a seguir )
a menos que considerarmos 1° M = 0 e depois diferente de zero . Veremos isto a seguir ) 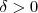
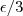 ,então por transitividade [Se
,então por transitividade [Se 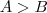 e
e 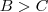 então
então 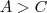 ] o resultado segue . E é isto que vamos fazer .
] o resultado segue . E é isto que vamos fazer .  . Assim dá hipótese dos limites existirem , segue de (i) e (ii) que existe
. Assim dá hipótese dos limites existirem , segue de (i) e (ii) que existe 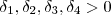 para os quais
para os quais 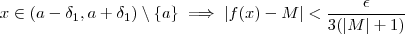

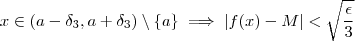

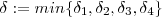 . Note que
. Note que 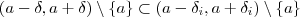 para cada
para cada 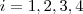 (Pq?) .
(Pq?) . ) [Usando a notação mais comum também é fácil ver ,
) [Usando a notação mais comum também é fácil ver , 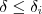 e se
e se  , por transitividade ,
, por transitividade , 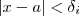 ](i=1,2,3,4).
](i=1,2,3,4). seque-se que
seque-se que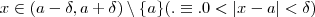 então todas implicações acima são verdadeiras . Daí ,
então todas implicações acima são verdadeiras . Daí ,  .
.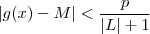 ao invés de
ao invés de 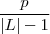 (pq isto automaticamente implica que
(pq isto automaticamente implica que  e podemos ter
e podemos ter  e
e 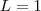 ) . Observe que troquei
) . Observe que troquei  por
por  , mas acho que não atrapalhará no entendimento .
, mas acho que não atrapalhará no entendimento .