6-(MED. JUNDIAI) Sejam as funções f e g , de R em R, definidas por
f(x) = 2x - 1 e g(x) = kx + t. A função g será inversa de f se, e somente se,
a)k - t = 1
b)k = 2t
c) k + t = 0
d) k = t = ½
não entende por que deu a alternativa d
sendo inversa f(x) e g(x)
f(x)= 2x -1
x/2 +1/2= y
g(x) = kx + t
x/k - t/k = y
por que o resultado da alternativa d
10-(ANGLO) Seja f(x) = 3x e f -¹ a sua inversa. A raiz da equação f(x) = f -¹(x)
é :
a)0
b) 3
c) 1/3
calculando:
f -¹ = x/3
f(X) =f-¹(x) = 3x = x/3 na alternativa da letra A, não sei como desenvolver para dar 0.
quem souber por favor me ajude. E até onde eu fiz está certo?


 com
com 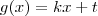 . Daí,
. Daí,  .
.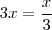 . Resolvendo,
. Resolvendo,

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)