Se
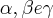 são raízes da equação
são raízes da equação 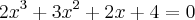 , então
, então 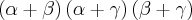 é igual a:
é igual a: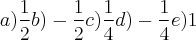
Gabarito: A

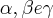 são raízes da equação
são raízes da equação 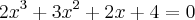 , então
, então 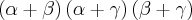 é igual a:
é igual a: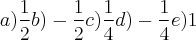

 teremos
teremos  (1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial 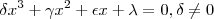 cuja raízes reais são
cuja raízes reais são  ,temos os resultados :
,temos os resultados : 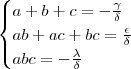 .
. 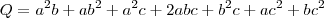 , segue
, segue ![Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)] Q = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/f7b1996e7a71532fe87986ec2566c5e4.png) e add
e add 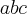 nos dois lados da igualdade
nos dois lados da igualdade ![Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)] Q +abc = [a(ab) + a(ac) + a(bc) ] + [b(ab) + b(ac)+ b(bc) ] + [c(ab) + c(ac) + c(cb)]](/latexrender/pictures/44f06630283829a20ee3f2a62ce46c6d.png) e assim obtemos
e assim obtemos  e portanto
e portanto 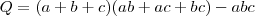

santhiago escreveu:Só por simplicidade vamos trocar alpha ,beta ,gamma respect. por a,b,c .
Expandindoteremos
(1) (muito obrigado Wolfram alpha ! ) ,agorá é só "brincar" com os a,b,c de modo a usar as Relações de Girard que estabelece uma relação entre as raízes de um polinômio e os seus coeficientes . De acordo com estas relações ,dada equação polinomial
cuja raízes reais são
,temos os resultados :
.
Seja, segue
e add
nos dois lados da igualdade
e assim obtemos
e portanto
Se não errei contas é isso . Tente concluir .

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.